平面ベクトル、複素平面、極座標
我々人間は平面上の図形で視覚的にものを考えるのが好きである。複雑なことがらを三次元で考えるのは少々困難であり、簡単なことがらでも四次元で視覚的に考えることは残念ながらできない。紙の上での、二次元の直交座標は十七世紀の数学を発展させた。ピュタゴラスの定理しかないのであるから、直交座標での一点 P の振る舞いはピュタゴラスの定理において常に同じであり、点 P をどのように呼ぶかによってベクトルであったり、複素数であったり、それらの極座標であったりする。ピュタゴラスの定理は三角関数と呼ばれる。三角関数の単位円での点 P (0, 1) は、ベクトルの (0, 1) 、複素数の i 、極座標の (1, π/2) と全く同じであり、したがって自由な互換性があるのは当然である。まず直交座標があり、そこでの点の表し方としてベクトル、複素数、極座標があるのであり、ベクトルの表現方法や複素数の表現方法として直交座標が用いられるのではない。ベクトルの平面や複素数の平面は三角関数の単位円を拡張しただけのものであり、直交座標での点 P は回転することができる。回転を中心を原点 O とするならば、点 P が 90° 回転するような操作をし、さらにもう一度 90° 回転するような操作をするならば、点 P とは逆の位置、点 -P となる。もしも点 P に -1 を掛けるならば、一気に点 -P となってしまうのであるが、言わば、半分ずつ、二回に分けて点 -P にする数が i である。直交座標における点 P を 90° 回転させる書き方の違いがベクトルと複素数の違いである。x2 = -1 の解を答えるときに、「もしも、数というものが原点 O のまわりをグルグルと回るものならば、そして、もしも 180° 回転したら反対側の数になるとするならば、90° 上の方、あるいは-90° 下の方です」と答えているのが純虚数 i であり、虚数というものに関して、神秘的な、あるいは不可知的な印象をもつ必要はない。なぜ i は縦軸なのかという質問はなく、x2 = -1 の解を「もしも数が回転するものならば、極座標 (1, ± π/2) のようなものです」と答えているだけなのである。まず純虚数 i が、二乗すれば -1 となる数としてのみ、狭く定義されただけであるならば、点(0, 1) のみが i の唯一の使われ方となるのであろうが、複素平面では i は縦軸の単位として広く定義され、複素平面の全体で使われ、(a + bi) のように実数との足し算の形で一点の値、ひとつの数を表す。また累乗にも自由に使われ、オイラーの等式にも使われている。 i という数は、だいたい 2.718 ぐらいを i 乗すれば、だいたい -0.043 ぐらいになるような、そういう数なのである。
・テイラー展開とオイラー等式の説明は、こちら。
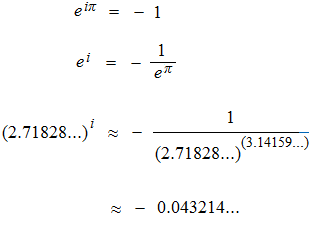
三角関数の単位円を拡張した直交座標の点 (0, 1) を i とし、(0 + i) という数で表すならば、そのような直交座標において、点 (1, 1), 点 (0, 1), 点 (1, 0) は、90° の回転とともに、1, i , -1 として表される。そのような直交座標、すなわち複素平面においてのみ、± i は x2 = -1 の解として意味をもつのであるが、複素数は実数も含むため、現在では一般的に実数から複素数へ自由に計算の領域を広げることか許されている。
