テイラー展開 オイラーの等式
模造の関数
テイラー展開、テイラー多項式、テイラー近似、どれも同じものです。
むずかしい関数の式を扱い易い多項式の形の式に作り変える方法です。今から三百年前には電卓などありませんでしたから、逆双曲線関数などで数値がでる場合は、実際に数値が欲しくて計算をする人達には、数値が出し易い、扱い易い模造の関数があればとても実用的だったはずです。テイラー展開は当時は必需品だったわけです。現在でもテイラー展開はコンピューターのプログラムで使われています。作り方を知るために、まず本物の関数の方もすでに多項式の形のものを例に採ります。
ニセの関数を Pとします。
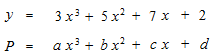
a = 3
b = 5
c = 7
d = 2
とすれば完璧なニセモノが作れるのですが、そうできるのは本物の方がそもそも多項式であるし、私達がすでに本物を知っているからです。ここではそのようにはせずに、微分を使ってニセモノを作ります。テイラー展開を使ってまねてみます。
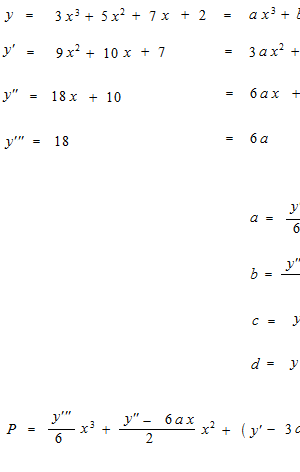
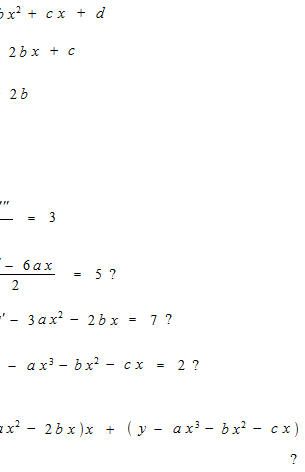
b = 5
c = 7
d = 2
にしたいわけですが、微分が同じなら導関数も同じというわけにはいきません。導関数の上下の位置が決まりません。積分定数 +Cがついてしまいます。一点をたとえば x = 0 のところで固定します。
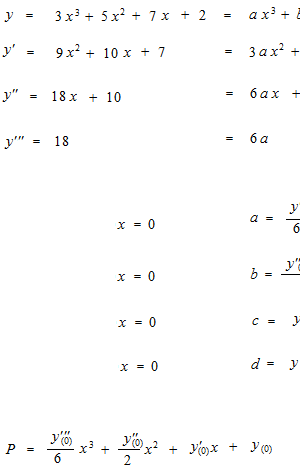
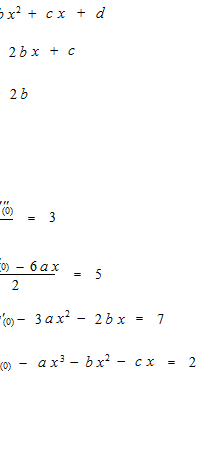
この例では本物が3次式なので3回微分をしたら完璧な模造ができました。
y = sin xのニセモノをテイラー展開を使って作ってみます。
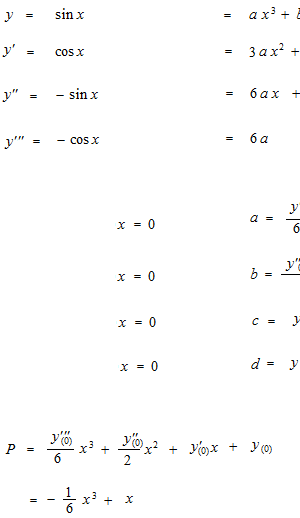
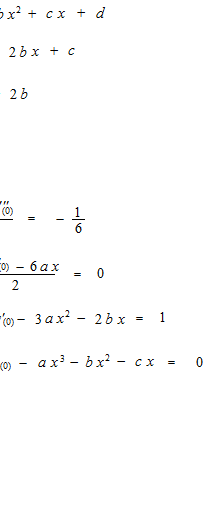
かなりひどいニセモノができました。誰が見てもニセモノとすぐにわかります。
たとえば
x = 6000
P(6000) = − 36 000 000 000 + 6000
-1 ≤ sin (6000)≤ 1
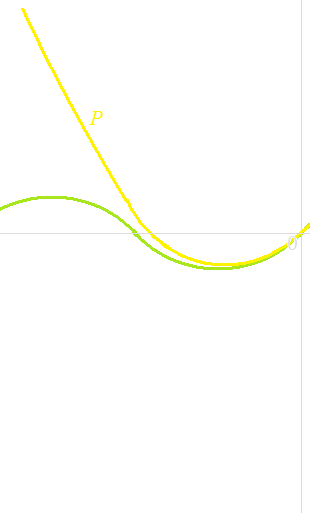
ところが 0 付近で見るとなかなかよくできています。
x = 0.1
P(0.1) = 0.09983333….
sin(0.1) = 0.09983341….
x = 1
P(1) = 0.8333333333….
sin(1) = 0.8414709848…..

テイラー展開を一般化します。
x = 0 を中心に作りましたが、任意の x = cを中心にして、つまり曲線を右に c 移動させて作ると一般化できます。
分母は導関数の作り方から階乗で表せます。
また、テイラー展開はだんだん次数を高くしていく式ですので、次数の低い順に項を並べるとつぎのようになります。
![]()
![]()
0! = 1
y を f に換えてから ∞ 次までをシグマ記号を使って書きます。
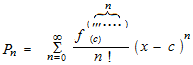
三角関数のサイン、コサイン、そして指数関数をテイラー展開すると下のようになります。
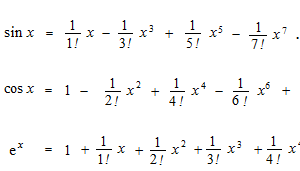
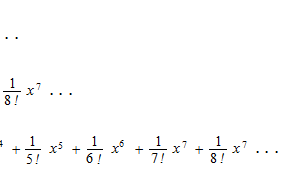
すこし工夫をすると指数関数をサインとコサインで表せそうです。
i = −1 を使います。オイラーの公式です。
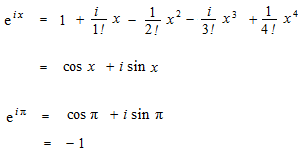
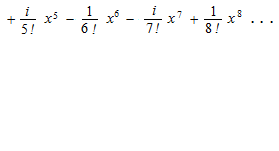
¤9
x が π のところでオイラーの等式になります。
