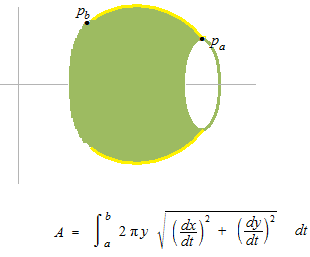Équation paramétrique
Soit un point P qui fait un mouvement circulaire à rayon R. La courbe dans le plan x-y ne sera qu’un cercle. Cela ne représentera pas le mouvement de rotation. En mettant le troisième axe pour le temps, la courbe sera en forme de ressort en spirale, ce ne sera plus un cercle. La longueur et l’aire de surface n’auront pas de bonnes valeurs. La courbe en trois dimensions sur une feuille de papier exige notre imagination. Si le point P faisait un mouvement en spirale en trois dimensions, il faudrait la quatrième dimension. Comme les maths cherchent toujours la simplicité, un ajout d’une dimension doit être éviter. La courbe est une visualisation d’une équation. Nous ne pouvons pas tracer une courbe sans équation. Comment pouvons-nous représenter un mouvement circulaire sans la représentation par une courbe?
Beaucoup de phénomènes naturels prennent un mouvement rotationnel qui n’est pas en un exact cercle. Pour cela, l’expression en x-y ne sera pas très bon choix, parce qu’il n’y a pas d’idée rotationnelle.
Les coordonnées polaires déterminent un point P du plan avec l’angle et la distance, ( r, θ )
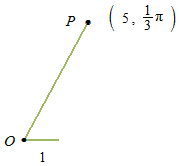
Le même point P peut être écrit en coordonnées cartésiennes.
x= rcosθ y = r sin θ
r2 = x2 + y2
Deux exemples de conversion entre une équation en coordonnées polaires
avec r , θ et une équation en coordonnées cartésiennes avec x, y .
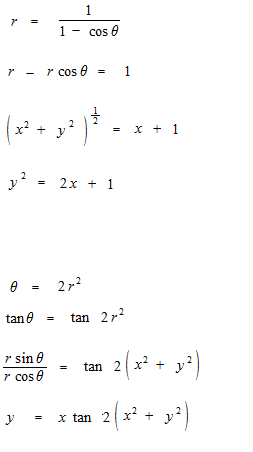
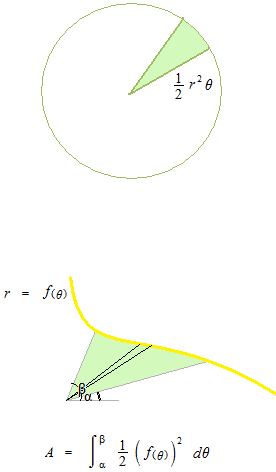
Pour calculer l’aire de surface enclose de la courbe d’une equation polaire, on utilise l’aire de secteur circulaire.
Exemple de l’aire enclose de la courbe d’une équation polaire. Dans cet exemple, l’equation n’est pas une fonction; l’aire est calculée en deux parties séparément.
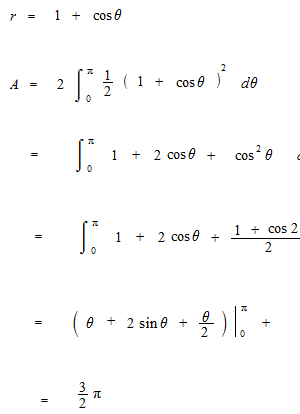
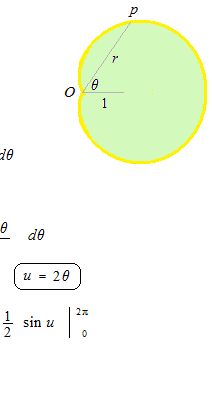
Équation paramétrique
Dans cette page, t est le paramètre. L’équation paramétrique, c’est une expression avec une autre variable.
D’abord il y a une équation normale qui a deux variable. x et y.
Une paire d’équations paramétriques expriment cette équation avec une autre variable.
x sera exprimé avec t seulement.
y sera exprimé avec t seulement.
Le point P qui fait un mouvement cerculaire à rayon R.
Il fait un tour en 2 secondes.
Voici une paire d’équations paramétriques.
x = R cos πt
y = R sin πt
Cycloïde droite
Voici l’équation paramétrique d’une cycloïde droite qui roule un tour chaque deux secondes.
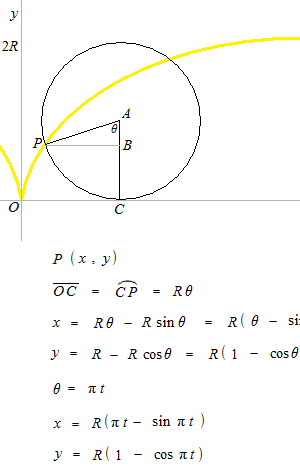
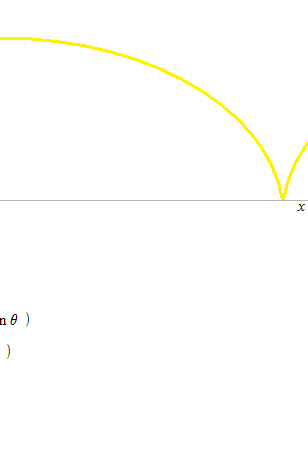
Longueur de courbe d’une équation paramétrique
Calcul intégral de la longueur de courbe de t = a à t = b .
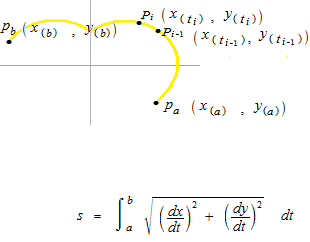
Si vous n’êtes pas sûr où se trouve dt , pensez plutôt à dθ.
En utilisant la longueur de courbe, on peut calculer l’aire de surface de révolution.