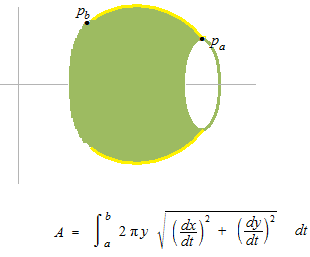パラメトリック方程式
半径Rの円運動をしている点Pがあります。x-y平面上のグラフにすると円になってしまい、回転運動を表すことはできません。三次元めのt軸をつくって時間の軸とするとグラフは螺旋のバネの形
になってしまい、円ではなくなります。長さや面積の値が違ってきます。紙の平面に描いた立体のグラフが見る人の想像力に頼らざるをえないことも否めません。もし仮に点Pがそもそも立体的に螺旋運動をしていたとするとグラフは四次元にもなってしまいます。数式をなるべく単純にすることを考えると次元をひとつ増やすことは避けたいともいえます。グラフは式の視覚化ですので、まず式がなければグラフは作れません。もしグラフがなかったとしたら円運動はどのような式で表されるでしょうか。さらに自然現象では円運動以外の回転運動が沢山あります。変数 x や変数 y には回転の考えがないので変数に中心角 θ を使ったほうが式は簡単になります。
極座標
極座標は角度と距離で点 Pの位置を表します。( r, θ )
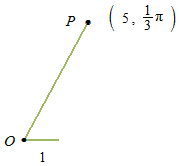
同じ点P を直交座標で表すこともできます。
x= rcosθ y = r sin θ
r2 = x2 + y2
r と θ を使った極座標の式を x と y を使った直交座標の式に変える例
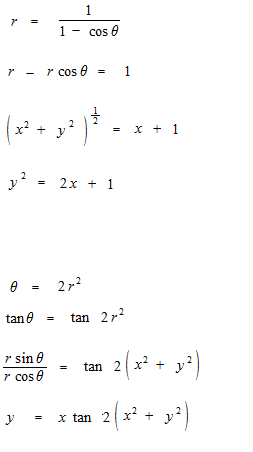
極座標の式の曲線に囲まれた部分の面積は扇形の面積を利用します。
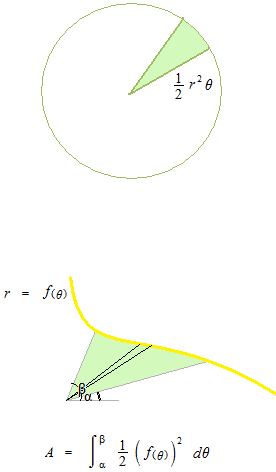
極座標の式の曲線に囲まれた部分の面積の例。この場合、もとの式が関数ではないので、上下に分けてから合わせます。
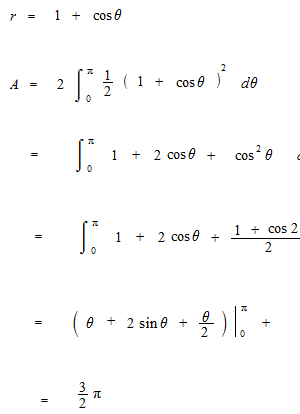
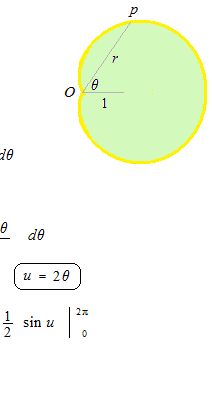
媒介変数表示 パラメトリック方程式
媒介変数をtとすると、パラメトリック方程式とは、まず普通のxとyの式があり、その x をt だけの式で、y もt だけの式で表したものです。半径 Rの円運動をしている点Pがあります。2秒で一回転する場合のパラメトリック方程式は下のようになります。
x = R cos πt
y = R sin πt
サイクロイド
2秒で一回転するサイクロイドのパラメトリック方程式は下のようになります。
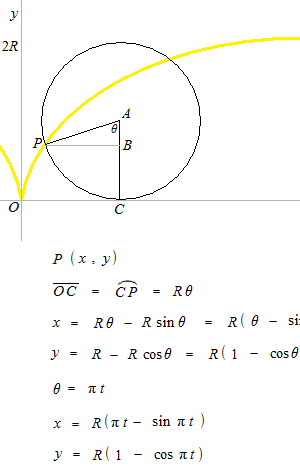
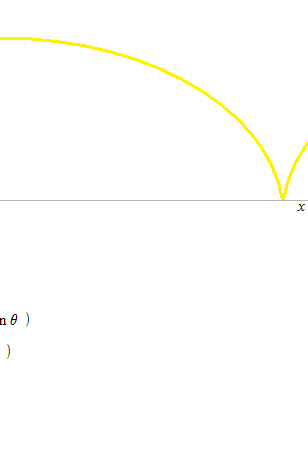
パラメトリック方程式による曲線の長さ
t =a から t =b までグラフの曲線の長さを積分で求めることができます。
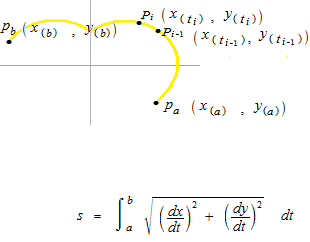
dt がどこにあるかが不明の場合はdθ と考えてください。曲線の長さを使って回転体の表面積が出せます。