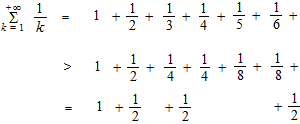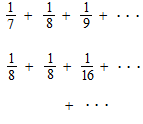無限級数
つぎの関数の曲線と比較しながら広義積分、数列、級数を見ます。まずこの関数の不定積分から始めましょう。
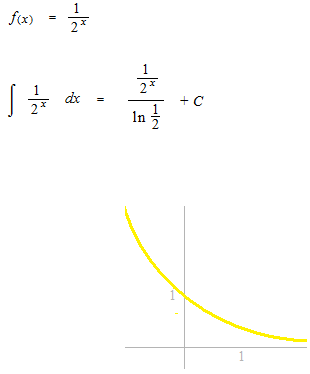
広義積分
閉じられた部分としてではなく、0 に近い隙間がありながら、極限として面積の値が数として出せる場合、即ち、収束している場合の定積分です。計算方法をではなく、定積分で出た極限値の値を広義積分と呼ぶので、「広義積分をする」と言ってはいけないようです。ここでは 1 以上の場合の面積の極限を計算します。
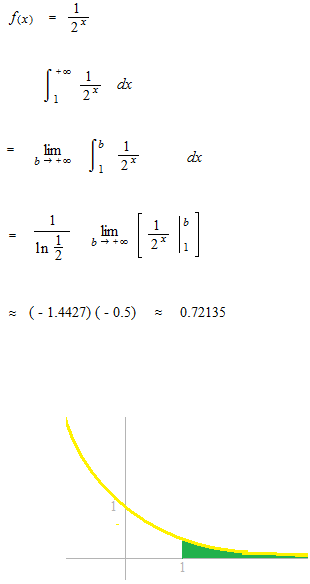
数列
xの定義域が正の整数のみであるような関数を数列とびます。
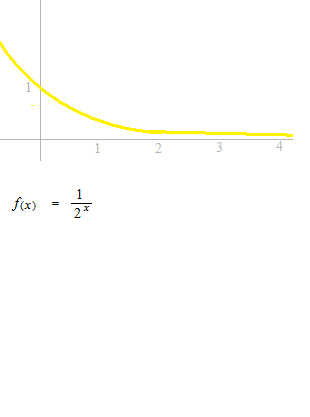
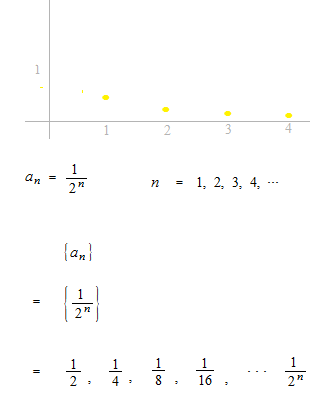
数列の収束
{sn}
| sn – L | < εすべての整数 n> N
極限がある場合を収束、ない場合を発散といいます。
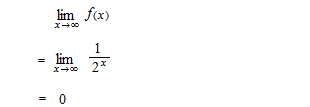
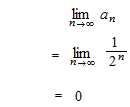
部分和
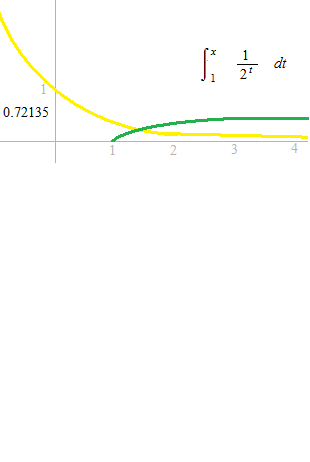
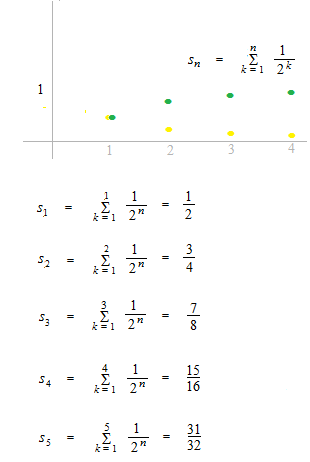
部分和の数列
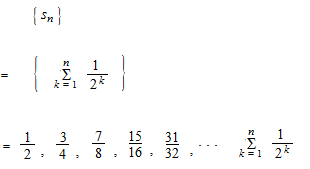
無限級数
部分和の数列の極限
級数の収束
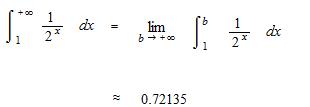
「数列の収束」と「級数の収束」を混同しないようにしましょう。

テレスコーピング級数
級数の式の計算そのものは、足し算、掛け算などのくふうによるものが多いようです。パズルです。
たとえば
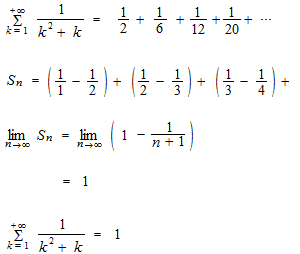
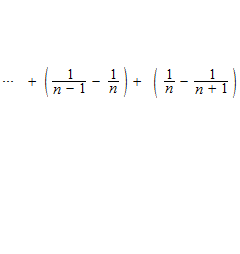
等比級数
同じ割合で変化していく数列を等比数列といいます。等比数列の和が等比級数ですが、比率 r が − 1 < r < 1 の場合は無限等比数列の和は収束します。たとえば
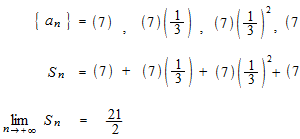
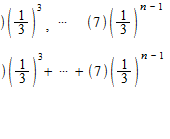
![]()
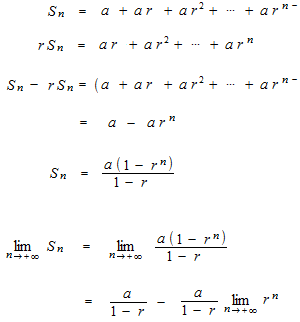
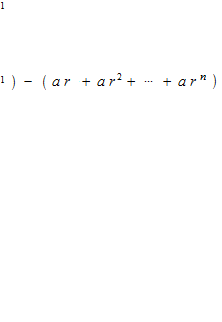
r = 1
Sn = a + a + a + ∙ ∙ ∙ + a = na発散
r = − 1
Sn = a − a + a − a + ∙ ∙ ∙ + an 発散
調和級数
![]()
![]()
調和級数は発散します。