Taylor polynomials, Euler’s identity
Taylor polynomials approximation
This is a method to make an imitation function that can be used as substitution when the original function is in difficult form to handle. Juste imagine the world of three hundred years ago where people had to do calculations with functions like reciprocal hyperbolic functions with no calculator in hand. False but substitutional functions were really helpful.
We’ll make an imitation function P.
In order to understand the method of manufacture, first of all, let’s see this example where the true function is already a polynomial function.
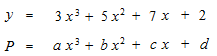
With
a = 3
b = 5
c = 7
d = 2
we have a perfect imitation function. It’s easy because the true function is a polynomial function itself.
However, there is a way to get these coefficients a b c d as using differentiation.
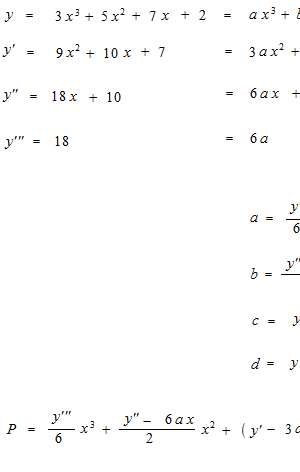
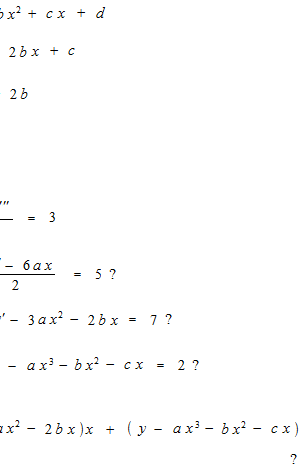
b = 5
c = 7
d = 2
But, if the derivatives are identical, we really have the same antiderivative? No, the vertical position would not be determinated. So we fix at a point, for instance at x = 0.
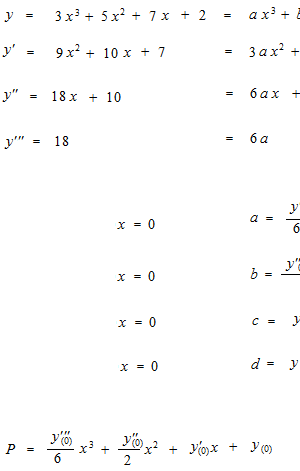
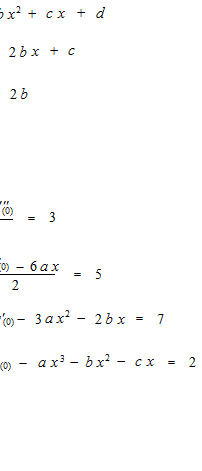
This example is a function of three degrees, after three differentiations, we obtain a perfect imitation.
This time, we make a false function of y = sin x
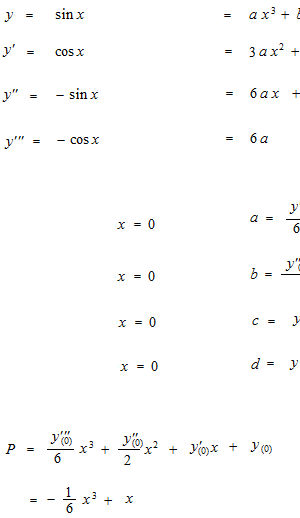
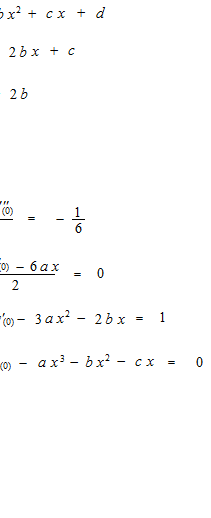
This time, we got a horrible imitation.
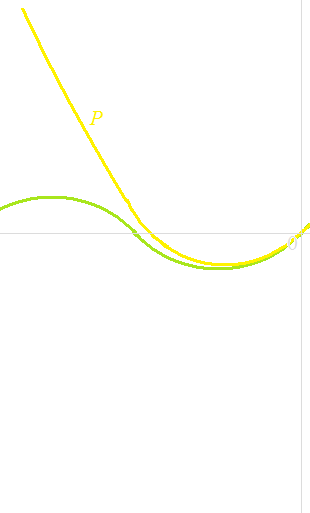
x = 6000
P(6000) = − 36 000 000 000 + 6000
-1 ≤ sin (6000)≤ 1
But close to 0, it is not so bad.
x = 0.1
P(0.1) = 0.09983333….
sin(0.1) = 0.09983341….
x = 1
P(1) = 0.8333333333….
sin(1) = 0.8414709848…..

Generalize the method.
The example has been made near x = 0, we can generalize the method. Imitation function will be made near x = c. That means shifting horizontally the curve toward the right. The denominators are written in factorial form. The terms begin with the lowest degree. Write f (x) instead of y. Infinite collection with sigma.
![]()
![]()
0! = 1
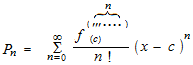
Here, we have Taylor polynomials of sine, cosine and the exponential function.
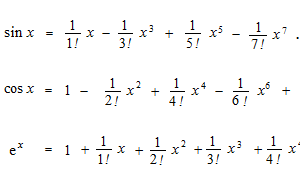
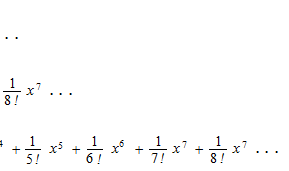
Everyone would try to write the exponential function with sin and cosine.
Euler used i = −1 . That is Euler’s formula.
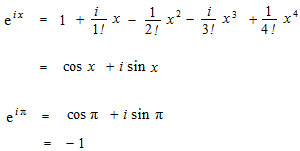
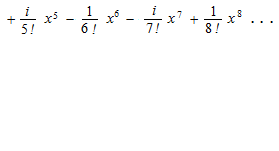
At x = π , the equation called Euler’s identity.
