Approximation polynomiale de Taylor, Identité d’Euler
Approximation polynomiale de Taylor
C’est une méthode pour fabriquer une fonction en forme facile qui pourra servir de substitution quand la fonction originale est difficile à manipuler. Pansez à ce qu’il y a trois cents ans, on n’avait pas de calculatrice pour effectuer des calculs comme fonctions hyperboliques réciproques etc. Pratiquement, de fausses fonctions étaient vraiement utiles.
Nous allons fabriquer une fonction en imitation P.Pour savoir la méthode de fabrication, ici, la vrai fonction est déjà une fonction polynomiale.
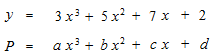
Avec
a = 3
b = 5
c = 7
d = 2
nous aurons une imitation parfaite. C’est facile parce que c’est une fonction polynomiale que nous voyons dèjà. Cependant, nous obtenons ces coefficients a b c d en utilisant différentiation.
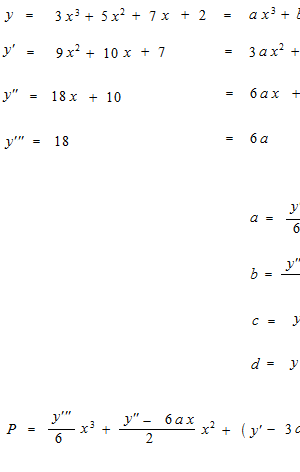
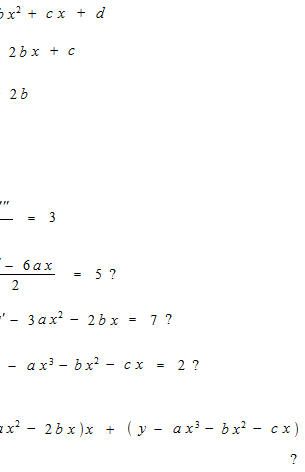
b = 5
c = 7
d = 2
Mais, si les dérivées sont identiques, nous aurons vraiment la même fonction primitive? Non, la hauteur ne sera pas déterlinée.
Il faudrait la constante d’intégration +C.
Donc nous fixons un point, par exemple à x = 0.
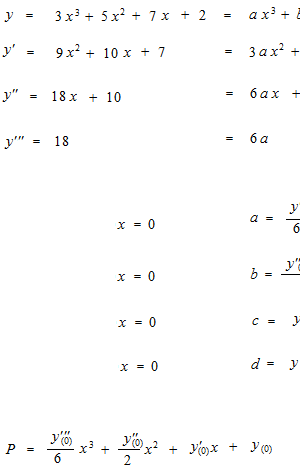
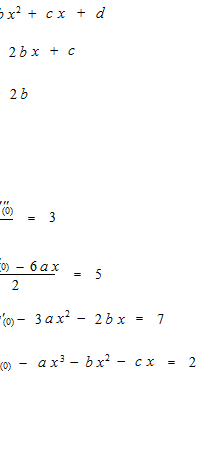
Comme cet exemple est une fonction en trois degrés, après trois différentiation, nous avons obtenu une parfaite imitation.
Maintnant, nous fabriquons une fausse fonction de y = sin x
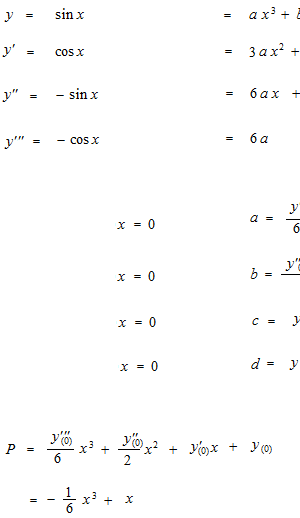
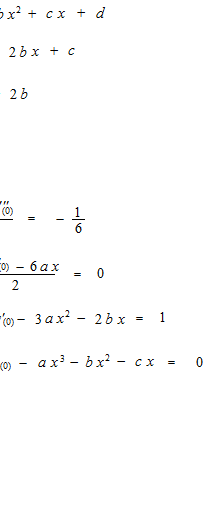
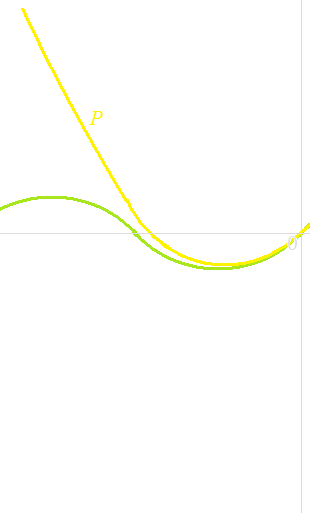
C’est une affreuse imitation .
x = 6000
P(6000) = − 36 000 000 000 + 6000
-1 ≤ sin (6000)≤ 1
Mais à proximité de 0, ce n’est pas si mal que cela.
x = 0.1
P(0.1) = 0.09983333….
sin(0.1) = 0.09983341….
x = 1
P(1) = 0.8333333333….
sin(1) = 0.8414709848…..

Généraliser la méthode
L’exemple a été fait à proximité de x = 0, nous pouvons généraliser la méthode en faisant à proxilité de x = c. C’est à déplacer la courbe horizontalement c vers droite.
Les dénominateurs sont en factoriel.
L’expression commence par le degré le plus bas .
![]()
![]()
0! = 1
Écrire avec f(x) à la place de y . Avec sigma jusqu’à l’infini.
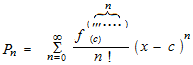
Voici, les approximations polynomiales de Taylor de sinus, cosinus et la fonction exponentielle.
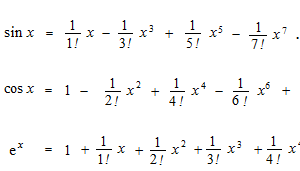
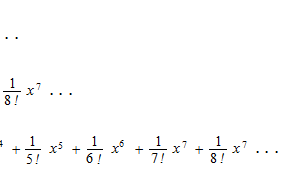
Cela donne l’invie d’exprimer la fonction exponentielle par sinus et cosinus.
On utilise i = −1 . C’est la formule d’Euler.
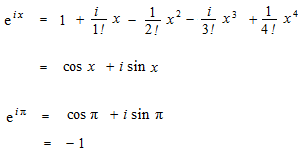
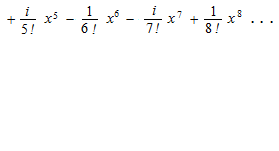
Quand x est de π , cela devient l’identité d’Euler.
