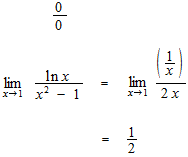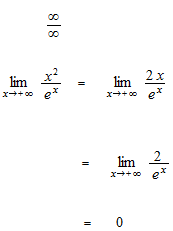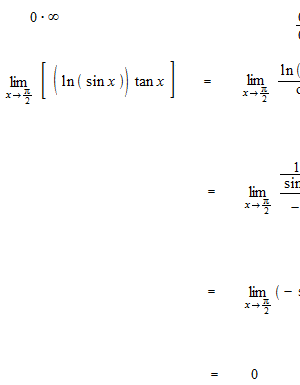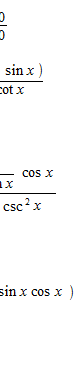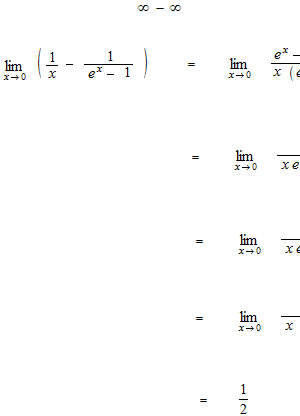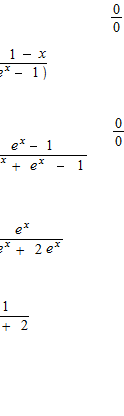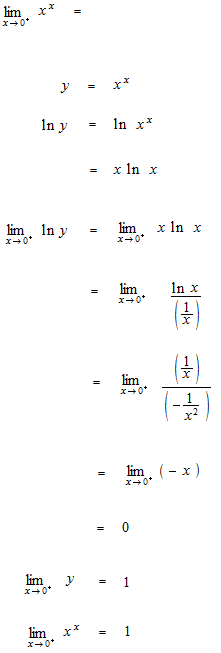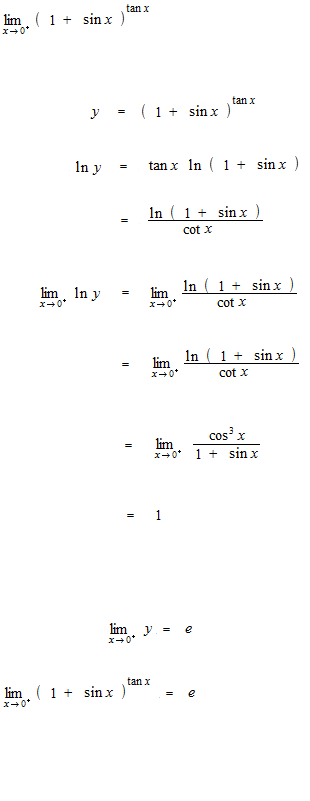Règle de L’Hôpital démonstration
Règle de L’Hôpital
Compréhension graphique et intuitive de la structure de la règle de L’Hôpital.
La règle de L’Hôpital est, en premier lieu, une conception très graphique. Les démonstrations avec epsilon-delta seront facilement comprises après ces représentations visuelles.
La règle de L’Hôpital peut résoudre la limite qui est en forme indéterminée, une forme de fraction dont, à la limite en question, le dénominateur et le numérateur sont tous les deux zéro, 0/0 , ou tous les deux l’infini, ∞/∞
La règle de L’Hôpital est très intuitive. Elle nécessite une représentation graphique de la dérivée.
Comment la dérivée d’une fonction apparaît-elle sur une courbe graphique?
Les dérivées sont des tangentes, aux multiples sens. La tangente, c’est la proportion de deux valeurs. Sur un graphique de dérivée, cette proportion est représentée comme une longueur. La unité “1” de proportion n’est pas la même unité que celle des ces deux valeurs. La dimension de dérivée n’est pas la dimension de longueur. Il faut un autre système de coordonnées sur une autre feuille de papier. Les questions confuses viennent de là; comme “Est-ce que dx a une certaine longueur?” ,etc. (dx est une grosse quantité au niveau de la proportion. Très souvent, nous l’utilisons sur l’axe temporel comme dt. Il y a des gens qui appliquent le temps à l’axe imaginaire.) Mais, les graphiques sont, d’ailleurs, nos magnifiques outils qui peuvent visualiser toute sorte de valeur. Nous devons en profiter la commodité librement en économisant le papier quadrillée.
Tangente
Après une différentiation qui s’est faite par le moyen de la limite, il ne s’agit plus qu’un point concernant la dérivée de la fonction. Il faut éviter de dire “au voisinage de”. Une tangente n’est plus que l’inclinaison de la ligne tangente à ce point. Ce point servira au paramètre de la variable sur l’axe horizontal de la dérivée qui est une fonction.
Nous allons tracer la longueur de tangente à côté de la courbe de la fonction. Considérez ce graphique comme un support sur lequel deux mondes sont réunis. Le calcul diffrentiel a essenciellement cette sorte de bizarrerie. Nous allons tracer la longueur de proportion.
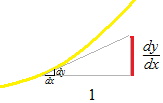
Théorème des accroissements finis de Lagrange
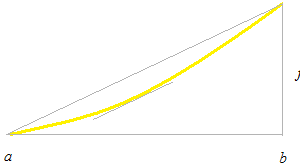
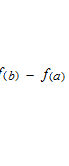
Il existe nécessairement, au moins, un point qui a une ligne tangente à l’inclinaison égale à la ligne droite qui passe par ces deux poins a et b.
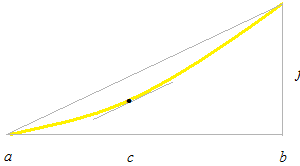
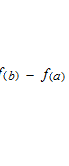
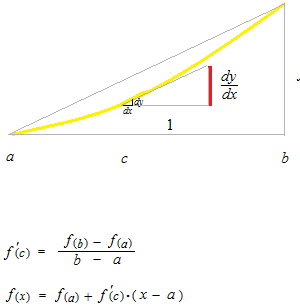

Cette équation sera rapparaître dans la page suivante comme les deux premiers termes de Taylor série. Cette équation du théorème des accroissements finis de Lagrange montre la pente du fonction avec sa dérivée. L’équation du théorème des accroissements finis justifie que la dérivée détermine la montée et la descente de la courbe de sa primitive. Le triangle qui a la base de 1 de longueur et celui qui a la base [ab] n’appartient pas au même système de coordonnées. Le petit triangle n’est pas à l’intérieur du grand triangle. Le point c restera toujours entre a et b même après l’opération de la limite et il sera utilisé comme la valeur de paramètre de la dérivée.


La combinaison de deux courbes du théorème des accroissements finis de Lagrange fait l’équation de Cauchy.
Règle de L’Hôpital
Nous abaissons f (a) et g(a) jusqu’à 0.
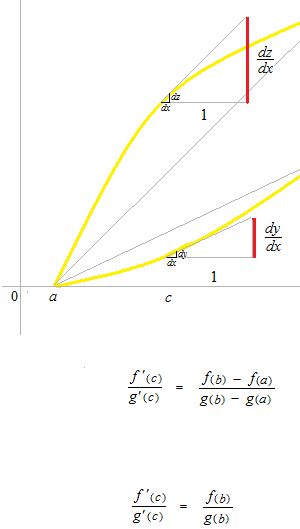
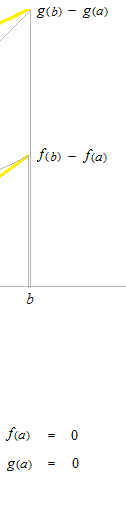
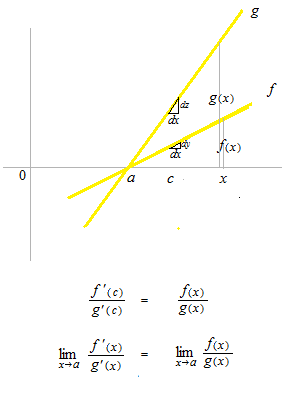
La règle de L’Hôpital pour résoudre la limite en forme indéterminée à un point c
le type 0 / 0 .
Les figures de la règle de L’Hôpital en symétrie latérale et verticale avec celle-ci seront traitées de la même manière.
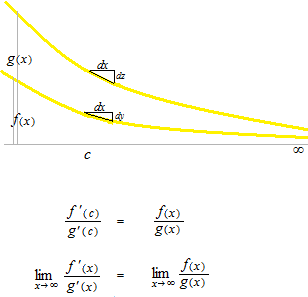
La règle de L’Hôpital pour résoudre la limite en formeindéterminée à l’infini le type 0/0
Les figures de la règle de L’Hôpital en symétrie latérale et verticale avec celle-ci seront traitées de la même manière.
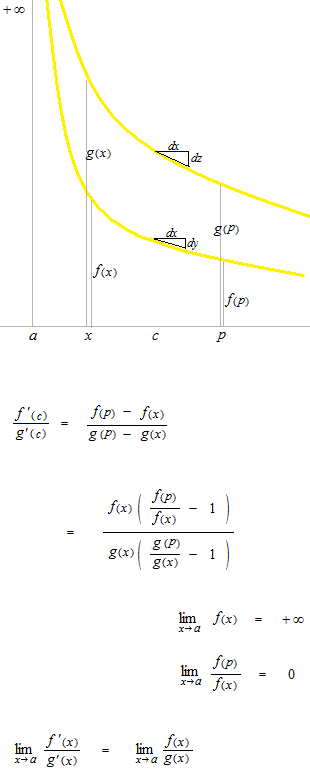
La règle de L’Hôpital pour résoudre la limite en formeindéterminée à l’infini
le type ∞/∞
Les figures de la règle de L’Hôpital en symétrie latérale et verticale avec celle-ci seront traitées de la même manière.
Des exemples d’application de la règle de L’Hôpital
¤11 16