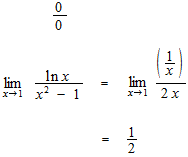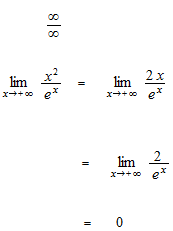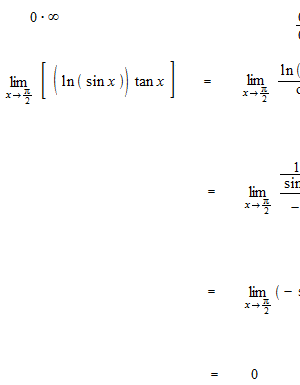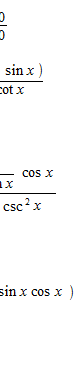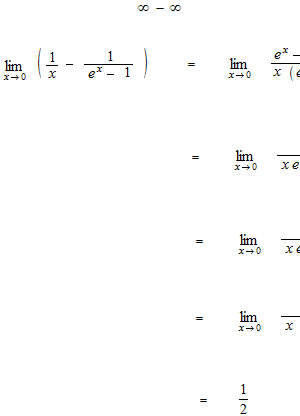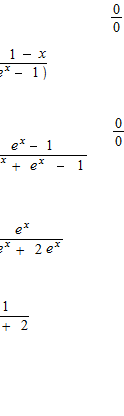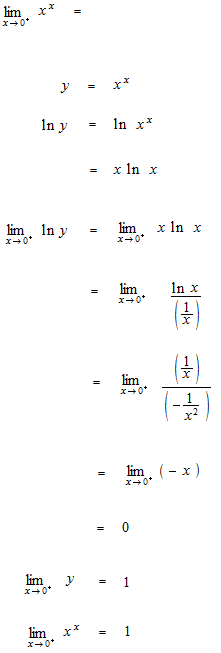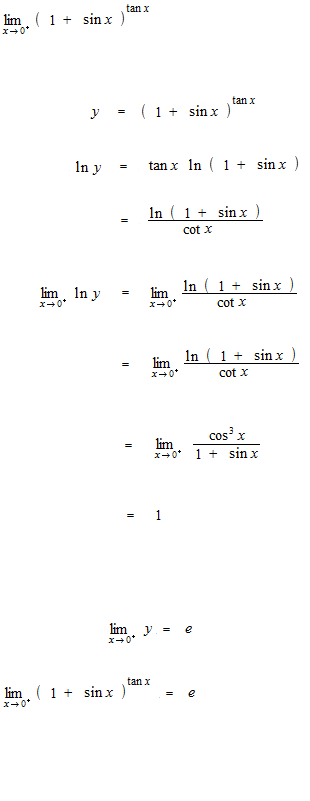ロピタルの定理の証明
ロピタルの定理の式の意味をグラフの形で直感的に理解しましょう。ロピタルの定理は、ラグランジュの平均値の定理の接線を使いますが、曲線も極限付近になると直線的になるといえるようなところから出てくる定理ですので、グラフでの理解のほうが式だけで表されるより容易です。ロピタルの定理は極限値の式ですのでエプシロンデルタの不等式で証明されますが、証明はグラフでの視覚的な理解が前提となります。ロピタルの定理は極限値を出す方法のひとつです。ロピタルの定理では、分数の形の不定形の極限値の計算方法が問題とされます。分母と分子が極限値を求めるところでそれぞれ 0 であったり、0/0 型、それぞれ無限であったりしたとき、∞/∞型、ロピタル定理を使うと簡単に解けます。ロピタルの定理の理解には導関数とは何かということの理解が大切なので、まず微分の復習、まとめとして、導関数とはグラフの曲線のどの部分のことかを見ます。
導関数はタンジェントです。ふたつの値の比率が 1 に対する値としてでます。グラフとしては、ふたつの値の比率がそのふたつのもののための座標とは別の次元に長さとして表されますが、これはグラフの表現方法の問題であり、視覚的理解の手段なので、ここでは便利さを優先させます。 また、dyや dx などが、長さか、あるいは比率の分子分母かという問いも答えはありませんが、ひとつの座標、一枚の方眼紙に納めようとしたときの問題といえます。 dx は比率の次元ではとても大きな量ともいえます。時間を軸にしたとき dt を使いますが、虚数の軸を時間の軸に使う人もいます。「比率の長さ」です。
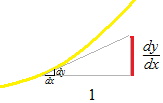
極限値の計算の結果は一点に於けるひとつの値になりますので、答えが出た後は、その付近での、という表現は避けましょう。一点における、その接線の傾きというしかありません。
ラグランジュの平均値定理
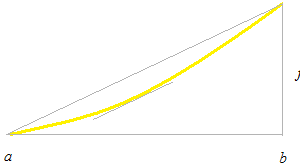
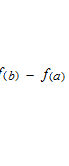
曲線上の二点間には、その二点を通る直線と同じ角度の接線を持つような点 c がひとつ以上必ずあるということから定理の式ができました。
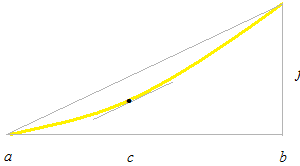
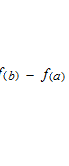
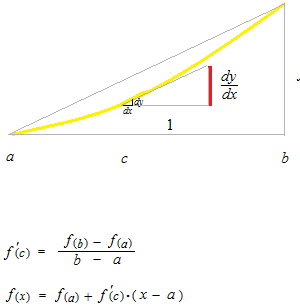

この等式は次のページでテイラー展開の初めの二項として出てきます。このラグランジュの平均値の定理を使ってグラフの曲線の上がり下がりが導関数のプラスマイナスで判断できます。底辺が 1 の三角形と底辺が [ab] の三角形は別の次元、別の座標で考えます。大きな三角形の中に小さな三角形があるわけではありません。極限値の話なので[ab] がとても狭くなり、それでも点cは最後まで間にはさまれ続けます。そのような点 c が [a, b] 間に必ずひとつ以上あります。また、このような点は、極限としてせばめていったときにも最後まで残る点なので、[a, b] 間というのを c で代表させて導関数のパラメーターにもなります。


ラグランジュの平均値の定理を二つ組み合わせればコーシーの平均値定理になります。
ロピタルの定理
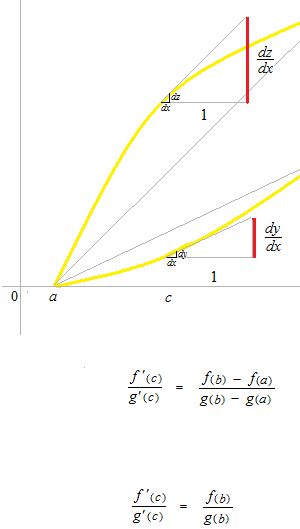
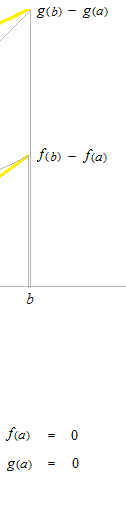
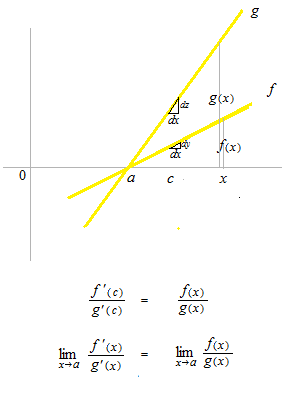
或る一点 a での 0/0 型のロピタルの定理は上のようになります。
左右対称、上下対称のロピタルの定理も同様になります。
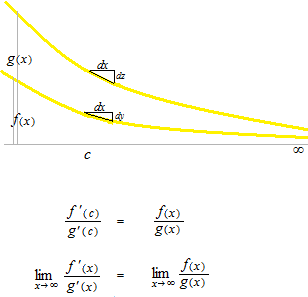
xが無限大での 0/0 型のロピタル定理は上のようになります。
左右対称、上下対称のロピタル定理も同様になります。
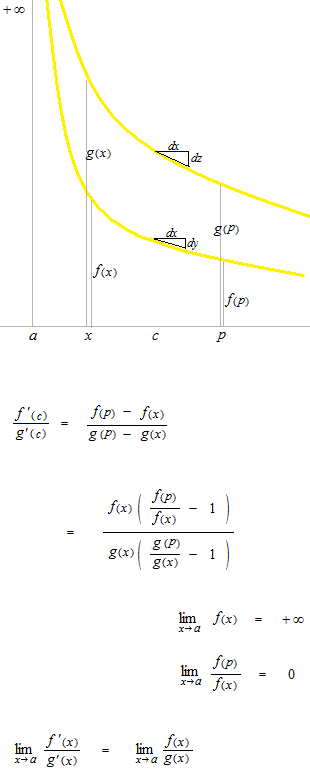
或る一点 a での∞/∞型のロピタルの定理は上のようになります。
左右対称、上下対称のロピタルの定理も同様になります。
ロピタルの定理を使った計算の例