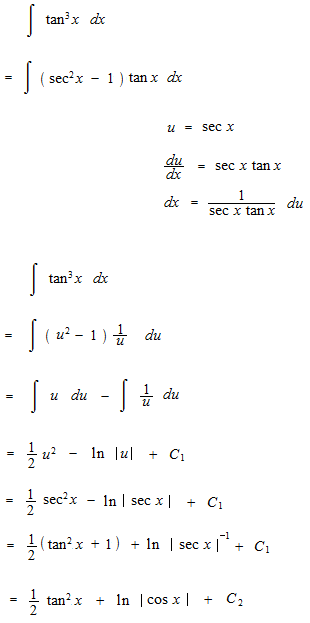Integration by parts
Find the derivative of this function using product rule.
y = ( x2 + 3 ) ( x4 − 5 )
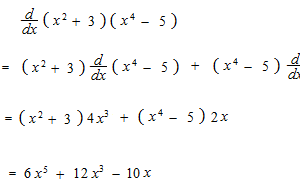
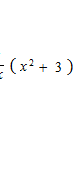
This formula of product rule has been found by Leibniz.
![]()
Now we integrate both sides of the equation of product rule.
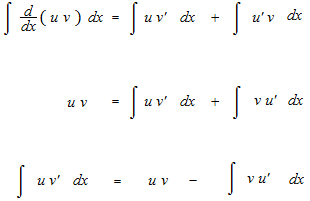
Even if we forget the formula, we can reconstruct it on the spot. This formula is called integration by parts. Sometimes, considering the term as uv’, the operation will be easily done.
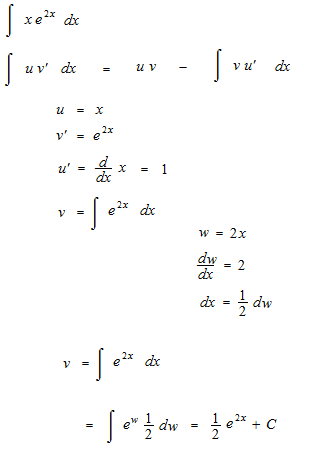
Constant of integration C in integration by parts ? Constant of integration C is very important for the understanding of the relationship between differentiation and integration. Should we write tha constant of integration C now or a little bit later? It’s embarrassing that we already use v when we are going to do integration of uv’ .
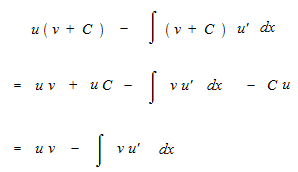
This constant of integration C is a number which does not make any sense on both sides of the equation. This constant of integration C should be eliminated from the equation.
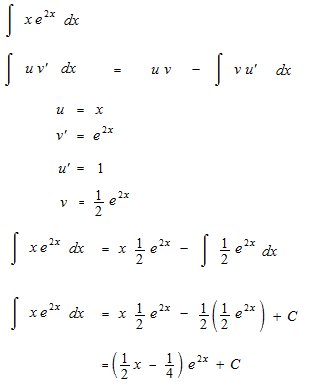
![]()
At this time, a constant of integration C is necessary in order that the equation would make sense.
Choice of u .
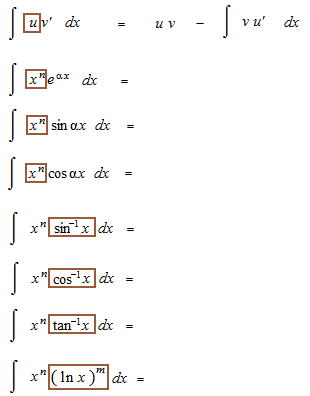
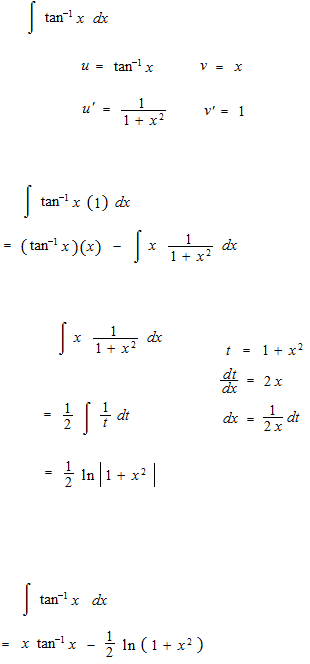
The formula can be written in another way.
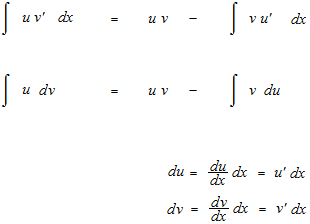
Let’s see integrals of sec x up to 5th power.
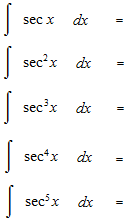

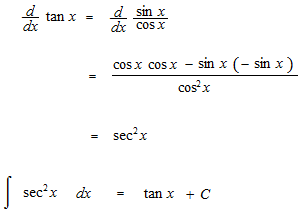
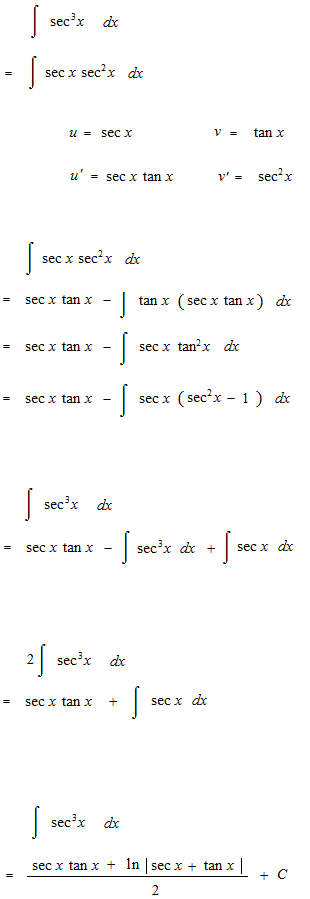
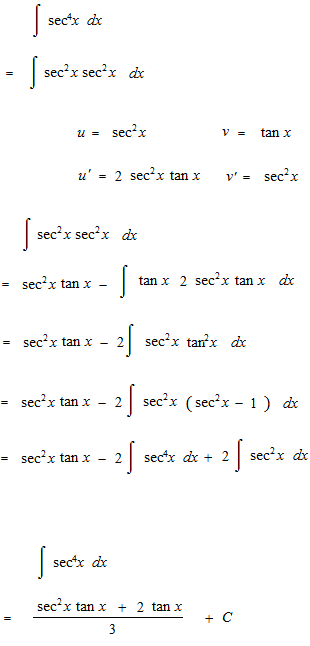
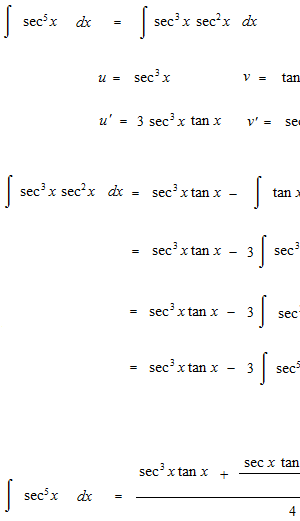
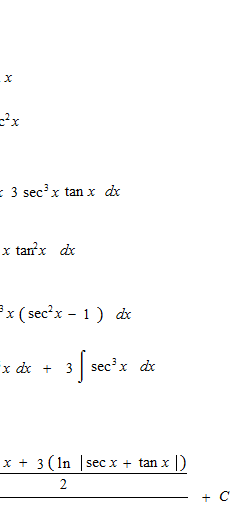
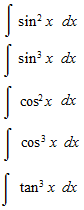
We are going to see the basis of the integratiion of trigonometric functions risen to the n-th power. That is question of way to make disappear the trigonometric function which comes out as a denominator.
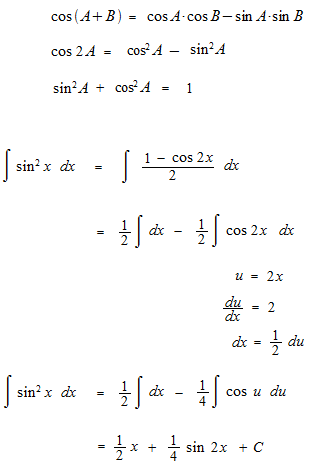
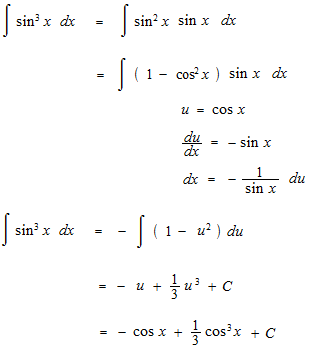
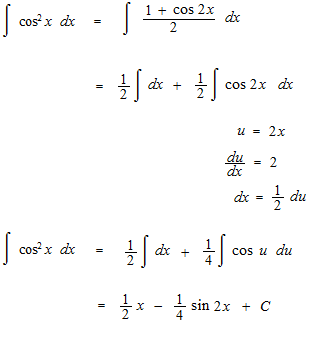
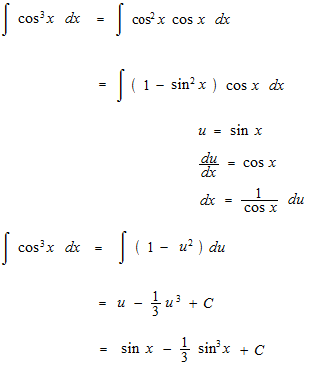
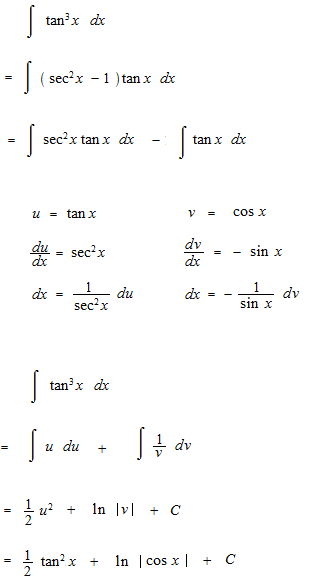
There is another solution.