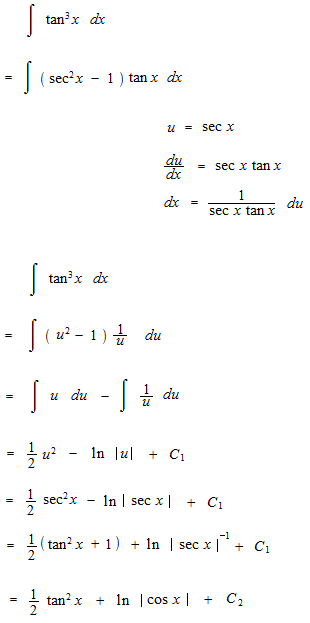部分積分の積分定数C
部分積分
y = ( x2 + 3 ) ( x4 − 5 )を積の微分の公式を使って微分。
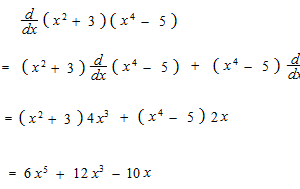
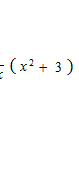
ライプニッツが見つけた積の微分の公式です。
![]()
こんどは、この公式の両辺を同時に積分します。
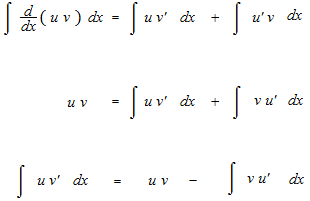
この部分積分の公式は、もし忘れたときでもその場ですぐに作れます。しかし、問題を見てすぐに部分積分が使えると気がつくためには部分積分をときどき練習しておく必要があります。
部分積分は積分の問題の式を uv’ とすると積分の計算が容易にできる場合に使います。Nous pourrions reproduire sur place cette formule d’intégration par parties quand nous l’avons oubliée.Cependant pour que nous vienne l’idée d’utiliser l’intégration par parties pour résoudre un problème, il faut que nous nous y habituions. Cela nécessite de la réviser de temps en temps. Si l’expression en question peut être considérée comme en forme de uv’ , l’intégration sera faite en utilisant l’intégration par parties.
例
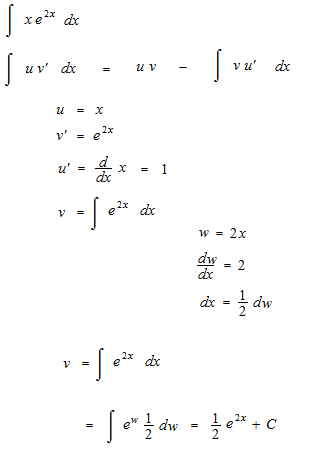
自身で紙に書いて覚えてください。部分積分の積分定数C は書きません。なぜでしょうか。部分積分の積分定数C の扱いは微分と積分の関係の理解の上でとても大切です。積分定数C をこんなところで付けていいものやら悪いものやら、きわめて重要な点といえます。
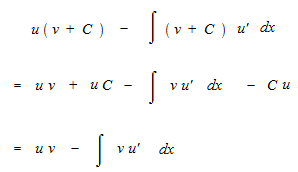
等式の両辺で積分定数 C が意味のないものとなります。
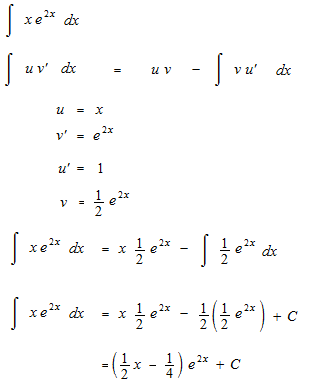
こんどは積分定数 C がないと等式になりません。
![]()
uの選び方
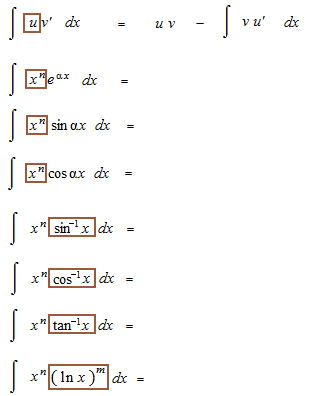
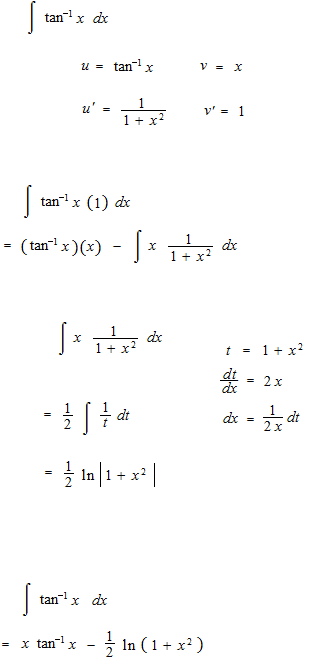
部分積分の公式の書き方はもうひとつあります。
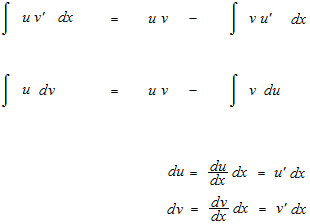
sec xを五乗まで積分します。
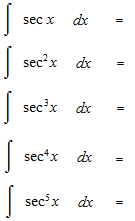

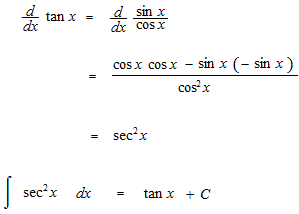
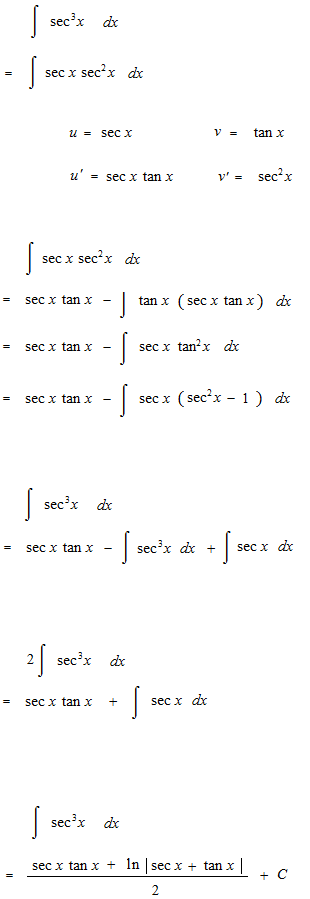
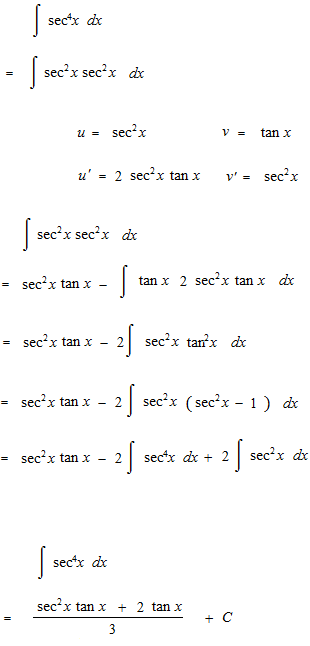
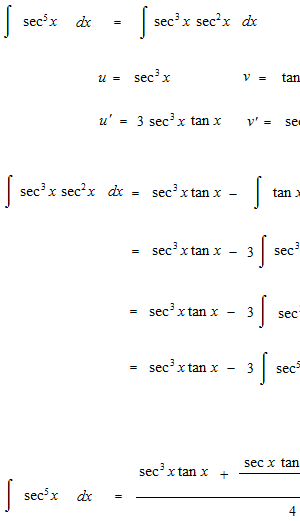
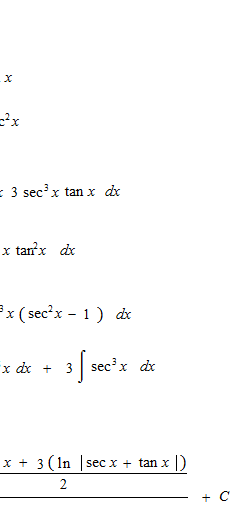
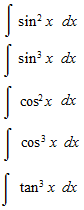
何乗かした三角関数の不定積分の仕方の基本的な部分を見ます。微分をすると分母の形で出てくる三角関数をどのように消すかという問題です。
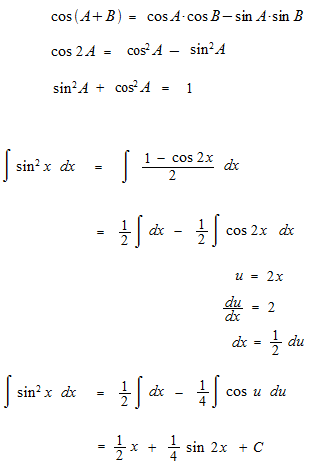
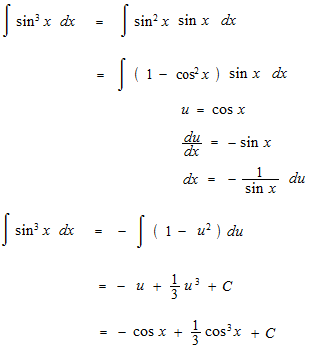
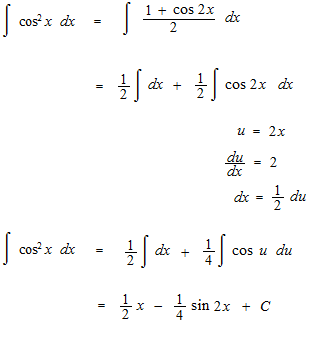
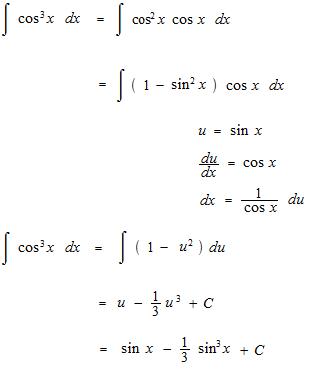
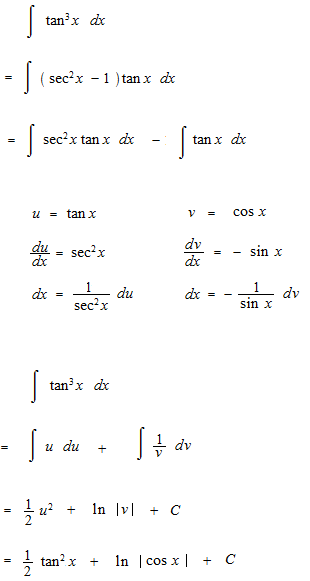
別の方法もあります。