Fonctions hyperboliques
Définitions des fonctions hyperboliques.
Les fonctions hyperboliques sont écrites avec une fonction trigonométrique et un h.
Cela nous fait penser inévitablement à quelque chose qui est en une étroite relation avec la grandeur d’angle. Cependant nous devons nous débarrasser de cette idée d’angle. Les fonctions hyperboliques n’ont aucune relation avec l’angle.
Aussi, la courbe de fonction hyperbolique est tout autre chose que celle de hyperbole. Une fonction hyperbolique n’a aucun rapport avec l’hyperbole.
Et la courbe d’une fonction hyperbolique est tout autre chose que la courbed y = 1/x
Nous jetons, d’abord, un coup d’oeil sur les courbes de deux fonctions hyperboliques.
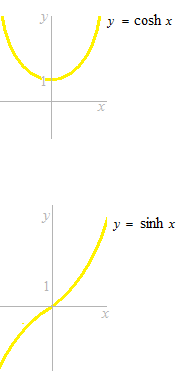
Hyperbole.
Maintenant, nous examinons l’hyperbole qui est tout autre chose que la fonction hyperbolique.
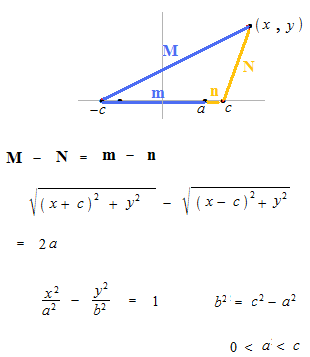
Il aurait fallu éléver au carré, deux fois.
Un exemple d’hyperbole.
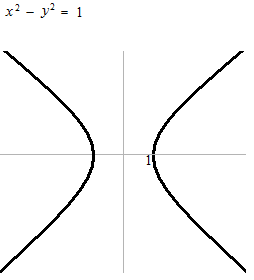
Ceci n’est pas une fonction.
Si l’on fait une rotation de la courbe de y = 1/x à −45° , est-ce qu’on aura une courbe d’hyperbole?
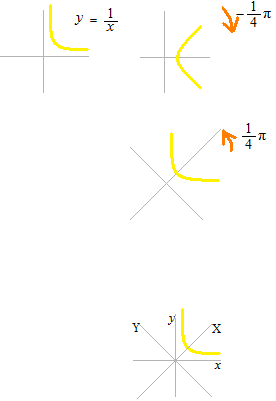
Pour faire une rotation d’une courbe, on fait plutôt une rotation des axes dans l’autre sens.
C’est comme un addition des angles dans sin et cos.
Regardez la rotation d’un point quelconque p à θ° .
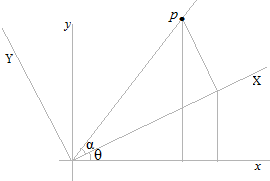
La position initiale du point p était exprimée en x-y. Ce point sera exprimé différemment en nouvelles coordonnées X-Y .
Qu’est-ce que nous allons chercher?
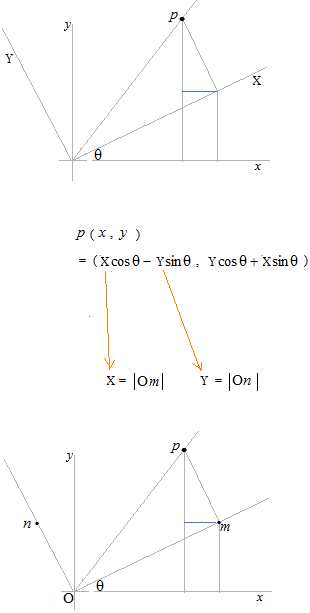
C’est ce qu’on voit très souvent dans les maths que s’il y a le nom d’un axe dans une équation, cela signifie, comme l’axe lui-même n’a pas de valeur, la valeur de ce point p sur cet axe.
Ce que nous allons faire maintenant, c’est d’exprimer p avec n et m.
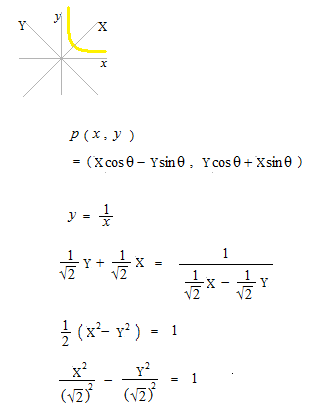
Nous avons maintenant une courbe d’hyperbole, mais elle est un peu plus grande que celle que nous
voulions: X2 − Y2 = 1 .
Nous cherchons la courbe plus petite en faisant tourner X2 − Y2 = 1 à 45° .
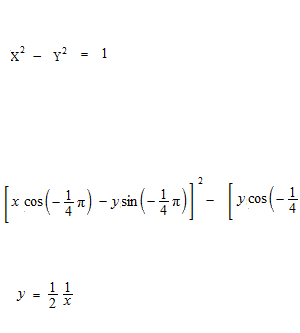
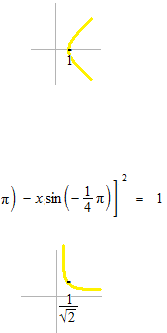
Nous utiliserons cette courbe un peu plus tard.
Reprenons la grande courbe de tout à l’heure.
Définition des fonctions hyperboliques sans utiliser la série de Taylor .
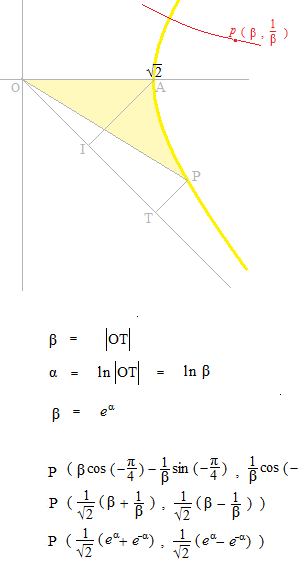
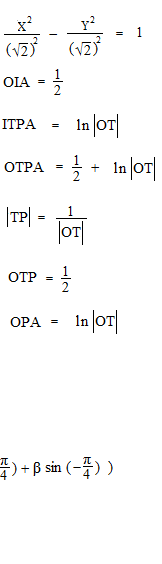
Nous rendons cette courbe plus petite.
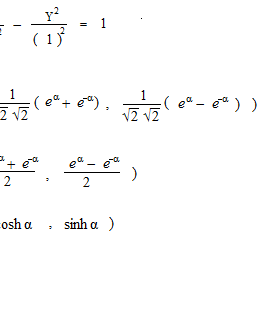
La diminution de l’aire est au carré de la diminution de la longueur.
![]()
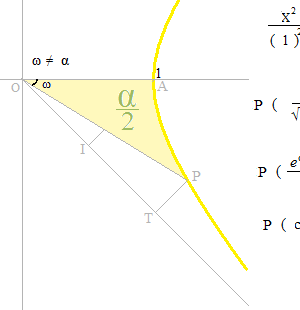
Les fonctions hyperboliques, ce sont des équations qui expriment la relation entre cosh α et sinh α qui font la valeur de l’aire de OAP la moitié de la valeur d’ α .
La grandeur de l’angle ω n’a pas de relation directe avec la définition des fonctions.
Les définitions des fonctions hyperboliques.
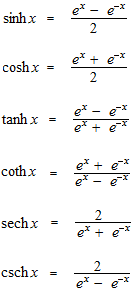
Dérivées des fonctions hyperboliques.
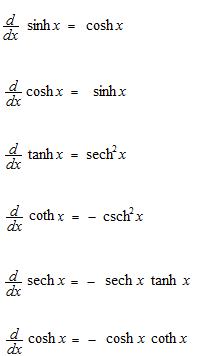
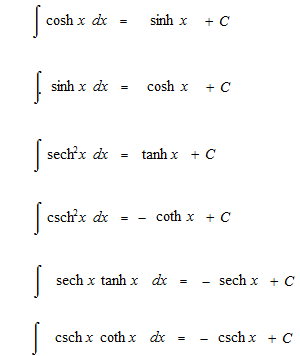
La différentiation de fonction exponentielle était comme ceci.
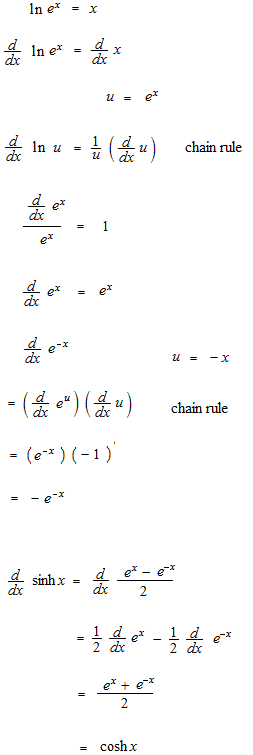
La série de Taylor est très facile. Lisez la page #42: Approximation polynomiale de Taylor, identité d’Euler et en suite, regardez ces équations.
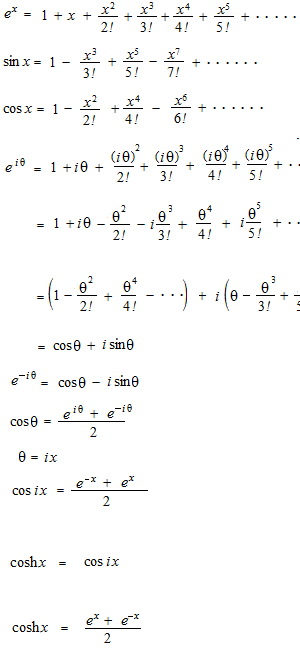
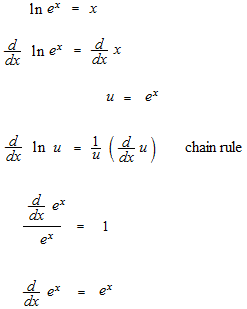
?
