双曲線関数の定義
sinh ハイパボリックサイン
cosh ハイパボリックコサイン
双曲線関数は三角関数に h の文字がついているので、どうしても角度と関係があると思ってしまいがちです。ところが、双曲線関数は角度とはまったく関係がありません。また、双曲線のグラフと双曲線関数のグラフとはまったく別のものです。双曲線関数は双曲線とはまったく関係がありません。さらに、 y = 1/xというグラフともまた違います。
それでは双曲線関数のグラフは、いったいどのような形をしているのでしょうか。
Definitions of hyperbolic functions
Hyperbolic functions are written with trigonometric function and an h. That makes us think of something that has a close relationship with angle. But we must get rid of this impression. Hyperbolic functions have no relationship with angle. And a curve of hyperbola and a curve of hyperbolic function are quite different things. There is no relationship between hyperbolic function and hyperbola. And also a curve of hyperbolic function is quite different from y = 1/x .
Just take a look at courbes of two hyperbolic functions.
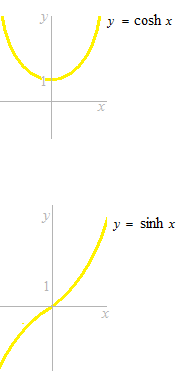
双曲線
それでは双曲線関数とはまったく違うものとして、双曲線のほうを見てみます。
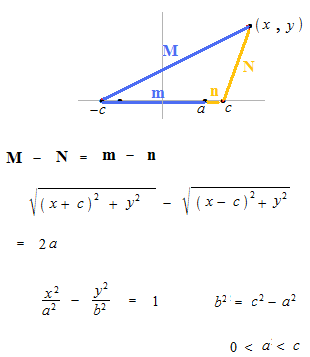
二回ほど二乗するはずです。
例
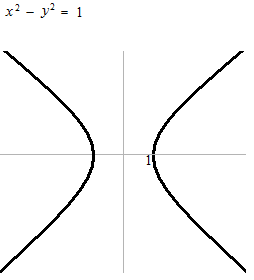
これは関数ではありません。
さて、つぎは y = 1/x のグラフです。
y = 1/xを −45° 回転させると双曲線になるでしょうか。
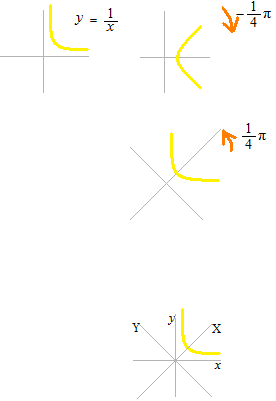
曲線はそのままで、座標軸のほうを逆に回転させます。
三角関数の角度の足し算と同じです。
まず、任意のひとつの点 p を θ° 回転させる方法です。
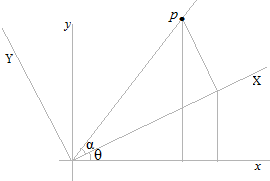
古い座標 x-yで表された点 p は、新しい座標 X-Y上ではどういう点 Pで表されるでしょうか。
どういう式が求められているのでしょうか。
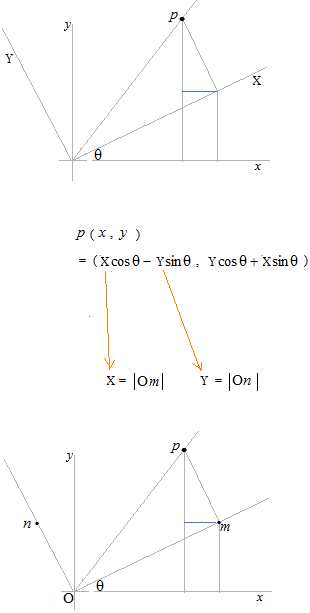
数学の式のなかで非常にしばしばみられることですが、軸の名前が一般の式のなかで使われているときは、軸そのものは値ではないので、 pのその軸上の値を意味します。
回転とは、つまり、On と Om の長さの関係の式のことです。
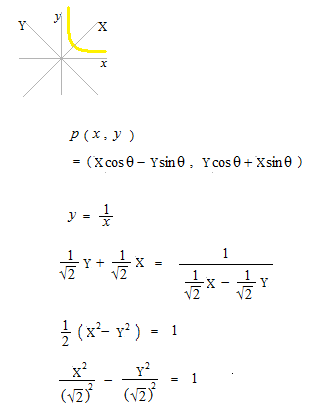
双曲線になりましたが、欲しい双曲線 X2 − Y2 = 1 よりもすこし大きすぎるようです。
逆に X2 − Y2 = 1 を 45° 回転させてみます。
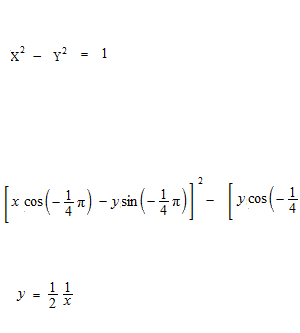
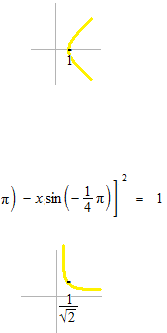
これはすぐあとで使います。
大きすぎるほうに戻って。テイラー展開を使わない双曲線関数の定義
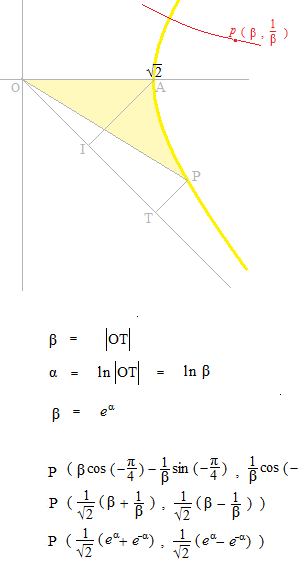
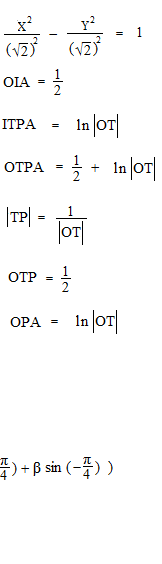
これは大きすぎる双曲線ですので小さくします。
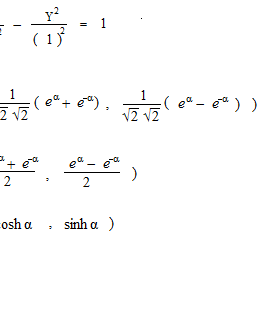
面積の変化は長さの変化の二乗です。
![]()
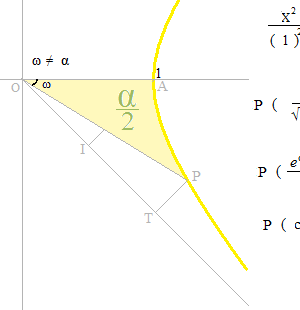
双曲線関数とは、P が ( cosh α , sinh α )のときOAPの面積が α の半分の値になるような関係の式です。
角度 ω は関数とは関係がありません。
双曲線関数の定義です。
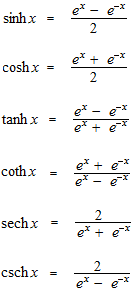
双曲線関数の微分
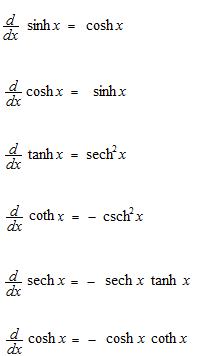
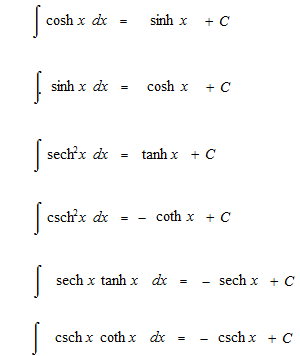
指数関数の微分を使います。
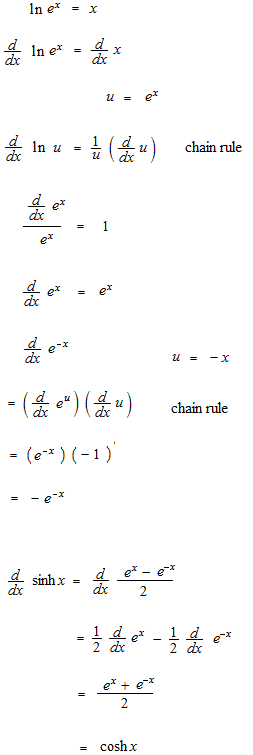
テイラー展開はとても簡単ですので #042 テイラー展開, オイラーの等式のページを読んでから下の式を見てください。
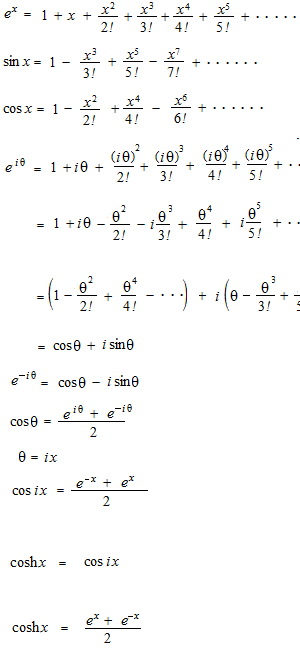
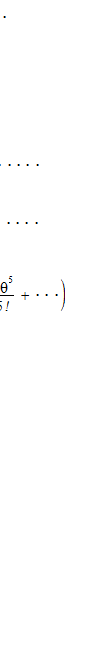
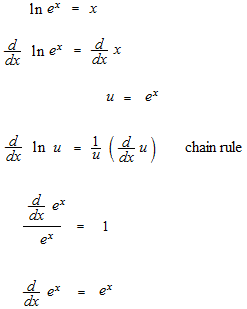
双曲線関数、 ハイパボリックサイン、ハイパボリックコサイン
