arc sine, arc cosine, arc tangent, arc cotangent, arc secant, arc cosecant
Inverse trigonometric functions
arc sine
arc cosine
arc tangent
arc cotangent
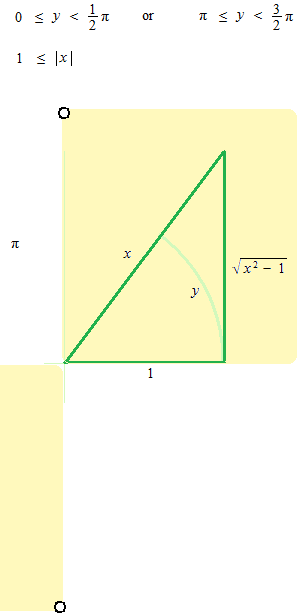
arc secant, inverse secant
arc cosecant, inverse cosecant
There are two ways to write inverse trigonometric functions
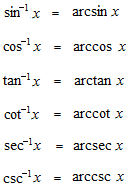
Domains of expression and derivatives of inverse trigonometric functions.
In order that the function would determinate only one value, inverse trigonometric functions must be written always with its domain of extression. These domains of extression have been only conventionally fixed.
arc sine
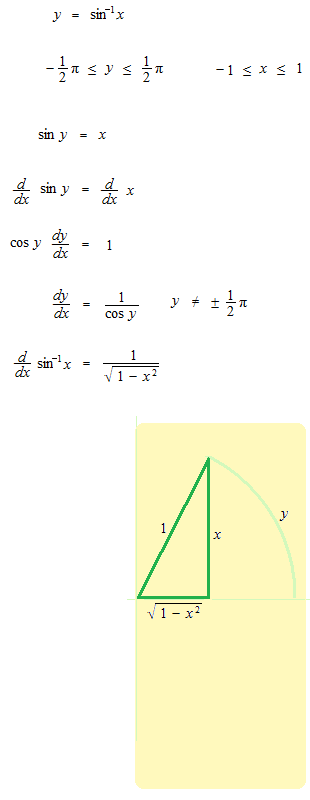
arc cosine
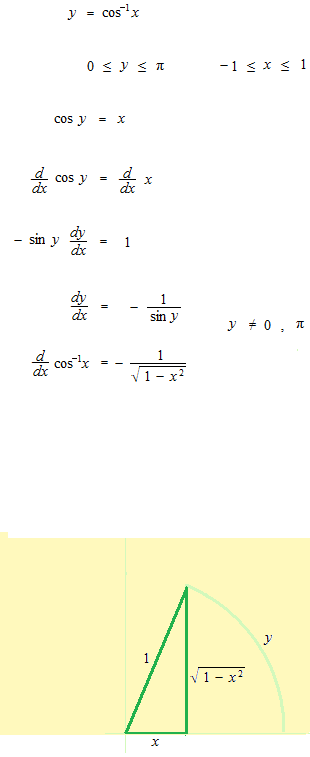
arc tangent
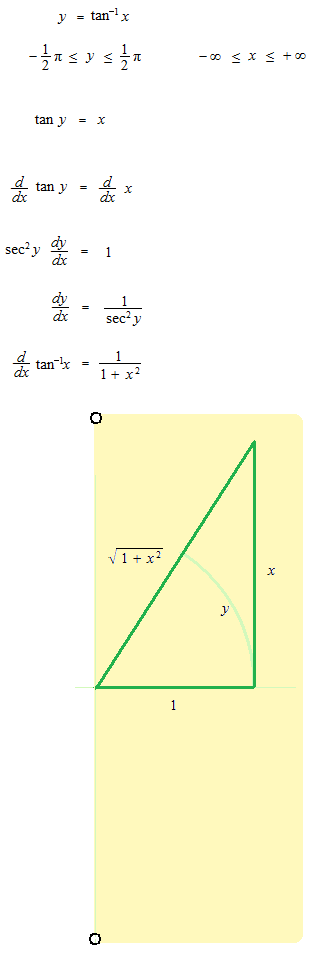
arc cotangent
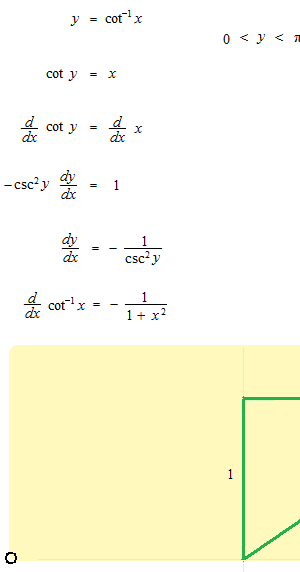

arc secant
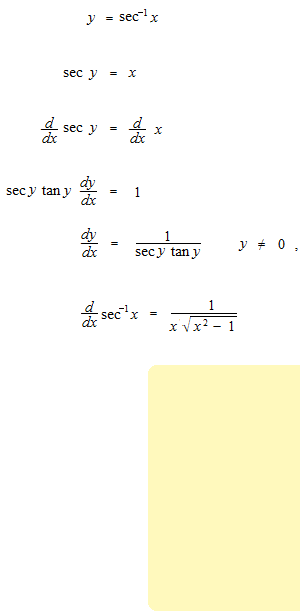
arc cosecant
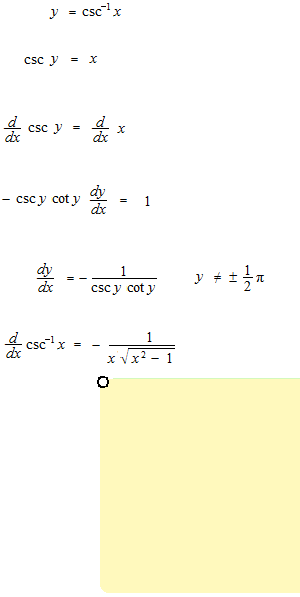
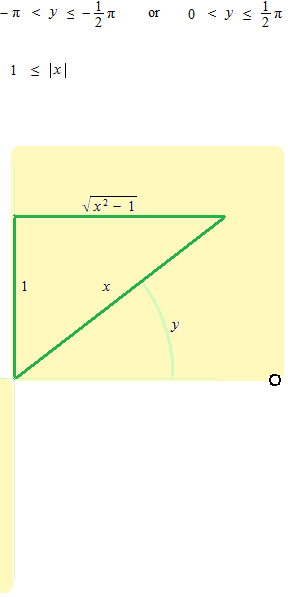
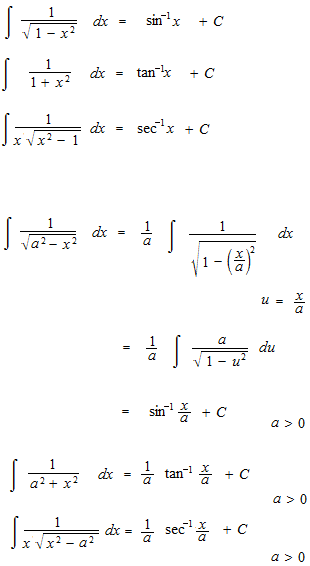
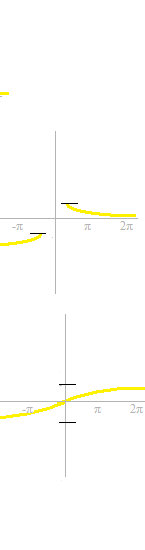
Examinate the length of a quarter of circumference

These are partial graphs of the six trigonometric functions.
If you are not yet familiarized with these curves of trigonometric functions, now’s time to memorize them.
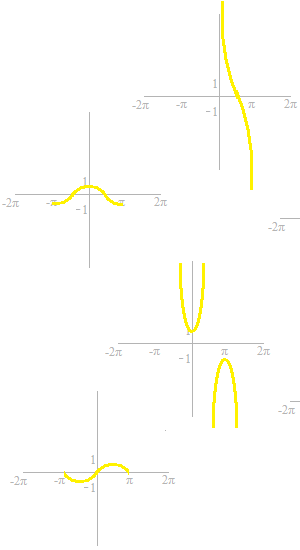
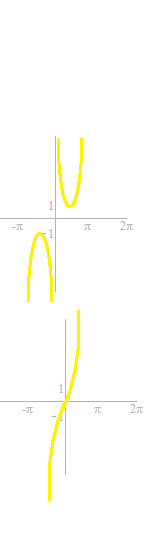
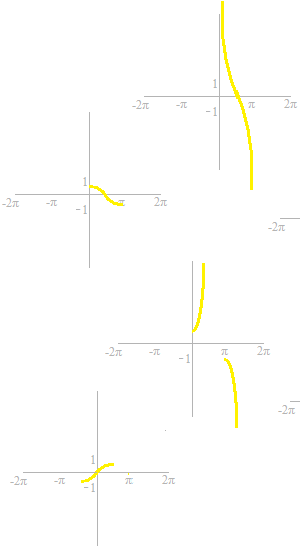
To get the inverse functions, straight lines of y = x are traced.
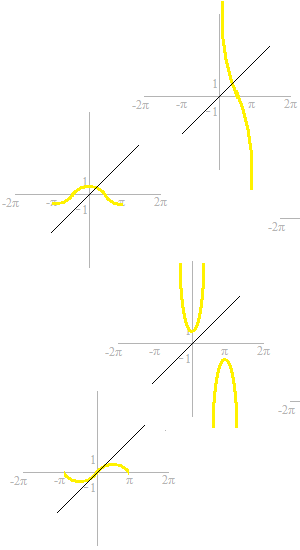
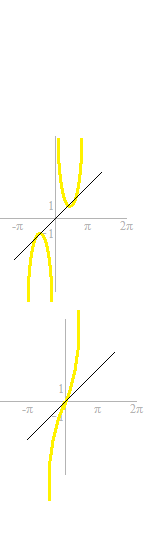
Curves which are symetric with respect to the line y = x are added.
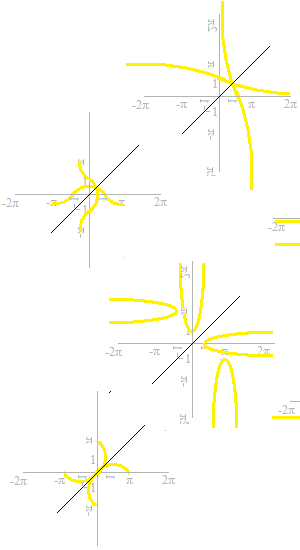
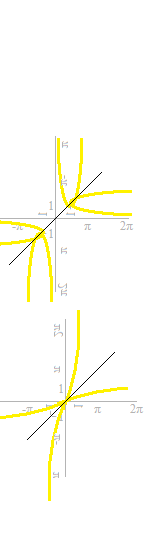
There are some curves which are not curves of a function.
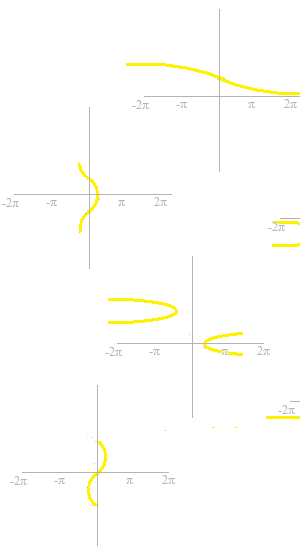
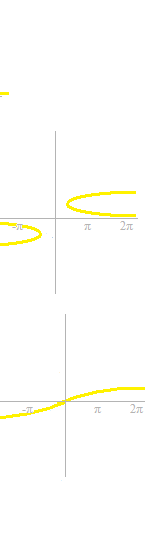
Let’s cut off the annoying parts.
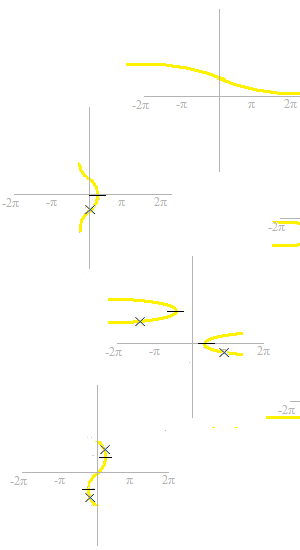
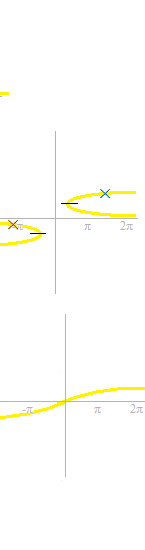
Now, they can be called functions.
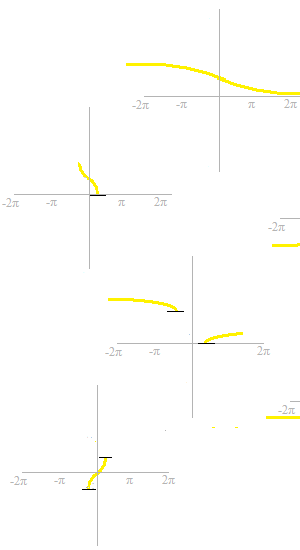

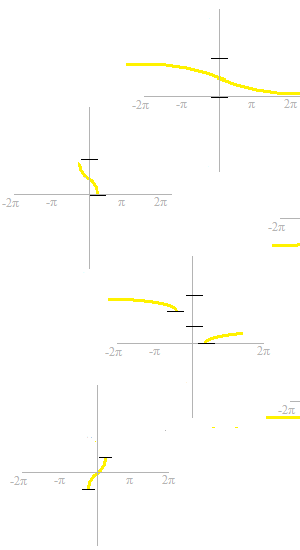
The corresponding parts of the graphs of trigonometric functions must be partially also cut off.
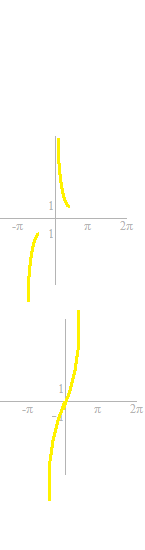
arc sine arc cosine arc tangent arc cotangent arc secant, arc cosecant
