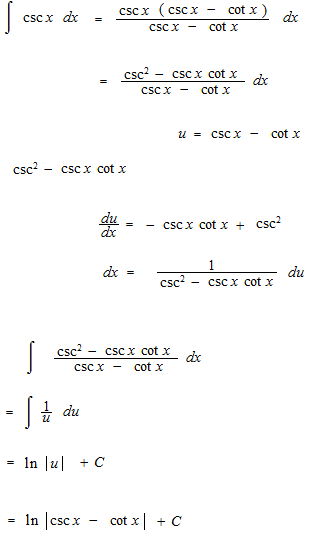三角関数の積分
まず微分積分の公式を暗記してからそれぞれの関数の構造を見ます。微積分の計算の結果の数値は非常にしばしば下の四つの形をとります。
三角関数
逆三角関数
双曲線関数
逆双曲線関数
この四つの関数は、積分の答えの表現方法です。
順序として、まず微分積分の公式を暗記してからそれぞれの関数の構造を見ます。全部で 43 ありますが、積分は微分の逆なので、23の公式を暗記するものともいえます。公式の内容は後で説明しますが、公式そのものは直感的理解を超えています。その人その人がそれぞれの暗記の工夫を考えます。きわめて個人的なことです。その人にとって容易な暗記の方法を見つけたときが、覚えたときということになります。このようなピタゴラスの定理の関係も暗記に使えます。
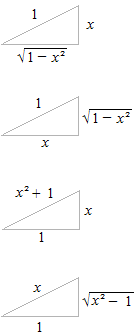
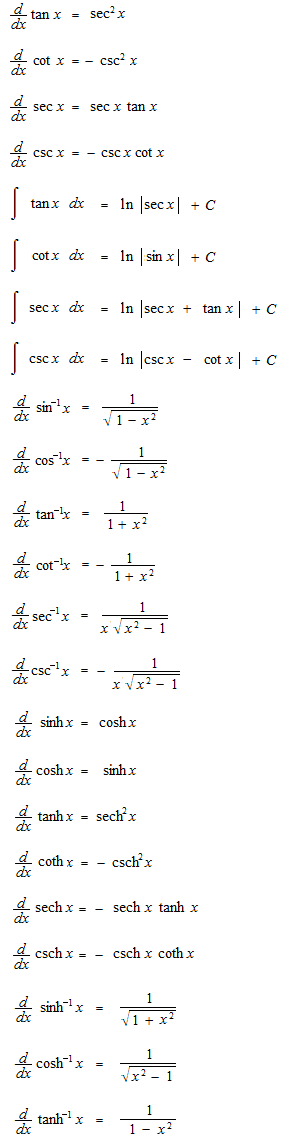
三角関数の単位円、三角関数のグラフ
三角関数の視覚化ということでは、単位円のほかに、三角関数のグラフというものがあります。
両方とも、とても便利ですが、ふたつ同時に思い浮かべると混乱しがちです。角度の表し方をみると、単位円では角度は中心角に於いて時計の逆まわりに増加し、グラフ上では角度は横軸の右の方向に増加します。関数の値は、たとえば cos は、単位円では横軸、グラフ上では縦軸であらわされます。単位円は三角関数の定義や計算の段階で使い、応用問題ではしばしばグラフ上で考えます。単位円での方向を全く忘れる必要も場合によってはあります。
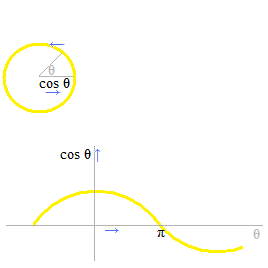
たとえば、次のような問題はどうでしょうか。或る大きな空港のなかの南北ふたつのターミナルをシャトルバスが結んでいます。2km 離れた直線の道路を分速 sin t km/ 分で走ります。乗客がいないので、一方のターミナルに着くと同時に反対のターミナルに向かいます。まず、南ターミナルから発車します。シャトルバスの南ターミナルからの距離をグラフに表してください。再び南ターミナルに戻って来るのは何分後でしょうか。ついでに、シャトルバスの加速度の関数も見ます。
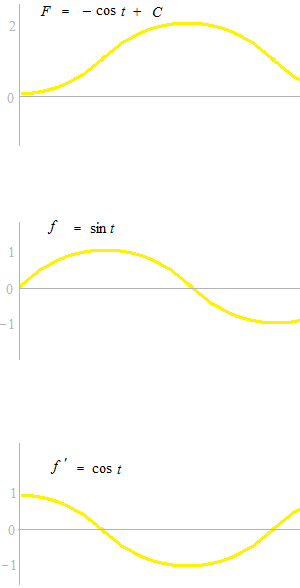
C = 1 の場合は上のグラフになります。
再び南ターミナルに戻って来るのは 2π分後。
三角関数の積分
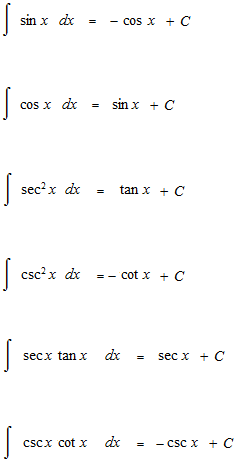
微分の逆で、可能な原始関数のすべてを表したものが不定積分です。三角関数の積分にはあと四つあります。
タンジェントの積分
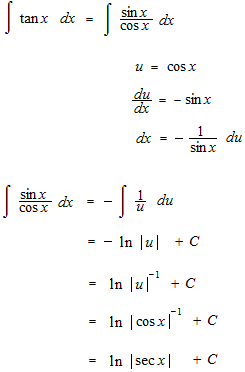
コタンジェントの積分
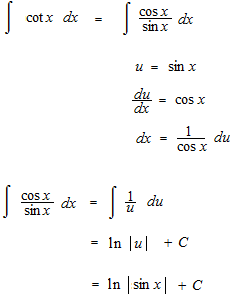
セカントの積分
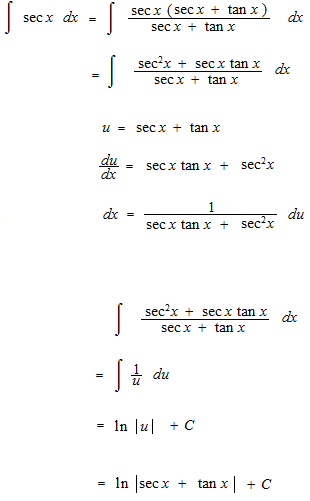
コセカントの積分