ニュートンの加熱の法則
ニュートンの加熱の法則とは普通はいいません。やはり冷却の法則というほうが正しいようです。法則というぐらいですから、使う数値が所々マイナスになったぐらいではびくともしない筈です。いきなり問題に向かうとプラスマイナスで混乱しがちですので指数関数のグラフの性質をしっかりと理解しておきましょう。公式を覚えてそれに数値を入れるだけでは面白くないので、なぜそうなるのかを考えます。
ニュートンの冷却の法則 加熱の場合
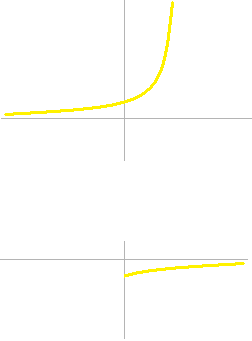
周囲の温度が 0 度でもっと冷たい物が 0 度に上昇していくグラフです。
銀行の利息と同じ指数関数のグラフですが、横軸の時間が逆、縦軸の温度の方向も逆です。
まず横軸の時間を逆にするのは前のページと同じで k≤ 0 とします。
N= N0 ekt
t ≤ 0 , k ≥ 0 ≡ t ≥ 0 , k ≤ 0
次に縦軸の温度の方向を逆にします。物体の温度が N0 から 0 に収束します。
N= N0 ekt k ≤ 0 N0 ≤ 0
銀行にたとえれば、利息がマイナスにつく銀行にお金を借りたところ、返す金額が減っていく状態です。いつも Aが 0°C というわけではないので、これを一般化します。
N−A= (N0 −A)ekt
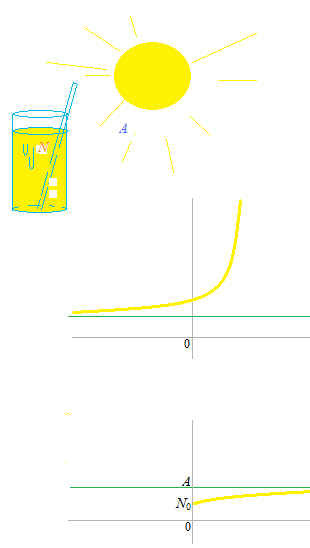
氷が入っていない冷たいオレンジジュース N°C。 初めは2°Cでした。
気温 32°C 、
8分後のオレンジジュースの温度 6°C、
さて15分後のオレンジジュースの温度は何度でしょうか。
場合によっては、時間とともに Nは Aと同じ値、あるいはそれ以上になるかもしれませんが゜、ここでは上のグラフのように考えることにします。
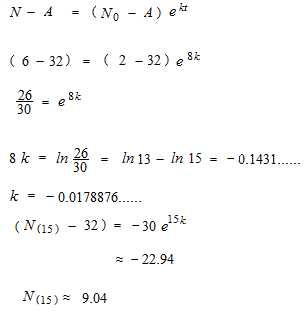
微分方程式の解法は既に公式のなかに含まれています。
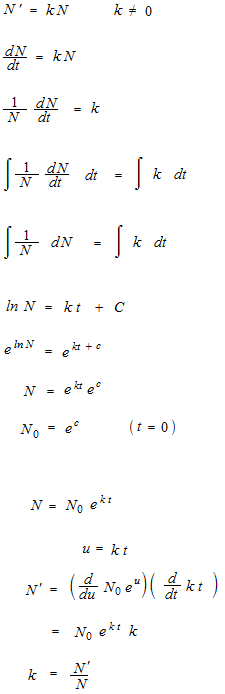
逆方向
