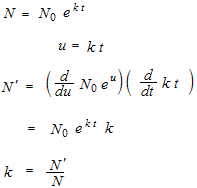Newton’s law of cooling
as an example of exponential decrease.
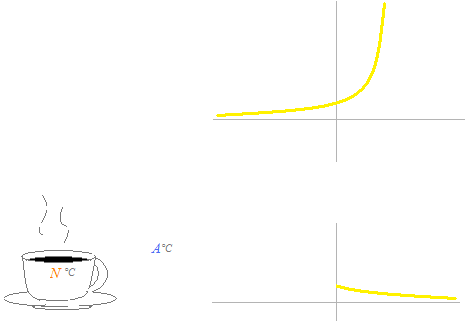
Let’s see the curve of Newton’s law of cooling when the temperature of object is N °C and surrounding air is at A °C . A °C can be a negative value. It is the conclusion out of the result of observations that Newton’s law of cooling is right. The influence of surface area and material nature of the object is included in coefficient k.
First, when A is at 0°C. It is the same curve as bank interest, exponentiel function, but the time is backward.
N = N0 ekt
t ≤ 0 , k ≥ 0 ≡ t ≥ 0 , k ≤ 0
Or, if it were a bank, it would be a bank that puts a negative interest and you would have less and less balance.
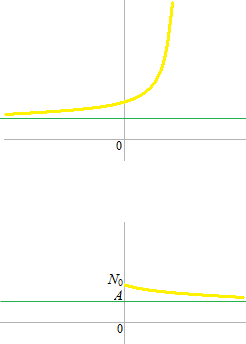
A is not always 0°C.
The generalized formula of law of cooling is like this.
N −A = ( N0−A) ekt
Graph translation
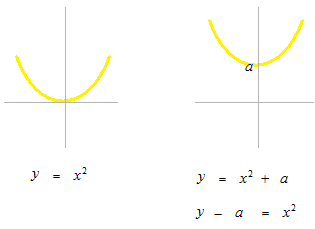
An example of calculation with Newton’s law of cooling.
A cup of coffee of 90 ° C is cooling in a room where the ambient
temperature is 25 ° C.
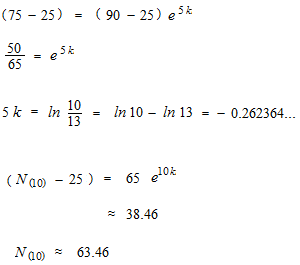
If, after five minutes, the temperature of coffee goes down to 75 ° C, calculate the temperature of coffee after 10 minutes.
Solution of differential function is already included in the formula. There is no integral calculation to find answer.
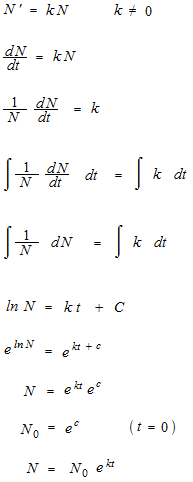
Reverse.