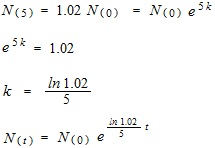変数分離型、1階常微分方程式; バクテリア繁殖
通常、方程式といった場合それは代数の方程式です。方程式はだいたい三つ四つの項でできていますが、この項のうちの一つを、あるいは二つを、導関数であるというふうに見なしたとき、その方程式は微分方程式であるともいえます。
たとえば距離 y とスピード v の式の場合。
自動車が出発点から 200km の距離を走る。
vt = 200
この代数方程式のスピードを、距離の時間に関する微分と見なすと微分方程式になります。
y’t = 200
微分方程式を解くとはその導関数 y’ の原始関数
y =
を書くことです。
y = 200
代数方程式も微分方程式も式それ自体は同じなのですが、この項が導関数だとしたらその原始関数は何ですかと問うのが微分方程式です。
積分をするときには、何かを導関数と見なしているはずです。
ふつうの代数関数のどの項を導関数と見なすかが問題となります。
ここでは数ページで定番の問題を見ます。
変数分離型1階常微分方程式の公式 N ‘ = k N
バクテリア増殖
ニュートンの冷却法則
炭素14
1階線型常微分方程式 N ‘ + k N = A
塩水
たとえば或る定関数があったとき、それを傾き 5 を表している式であるというふうに考えて、微分方程式から不定積分をして一次関数を書きます。
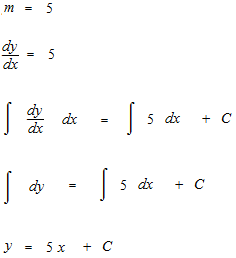
あるいは落下の加速度であると考えて、微分方程式を不定積分して落下速度の式を書きます。
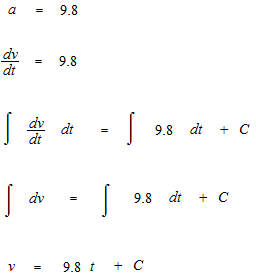
N = N0ekt
この銀行の利息の式は Nの導関数が使われていないので N の微分方程式ではありません。
下の形にするとNの微分方程式になります。
N ‘=k N
問題を解くときはすでに公式のなかに微分方程式が含まれているので微分方程式は使いません。
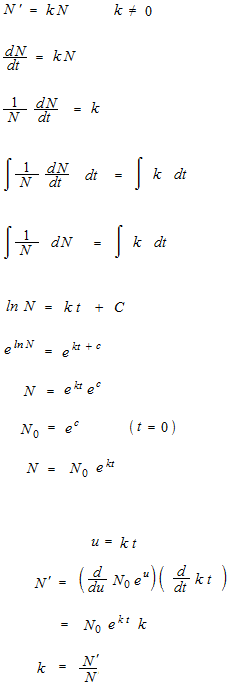
バクテリア増殖
或るバクテリア増殖が微分方程式で表されるということは観察の結果、あるいは微分方程式を考えるときの例としての仮定です。数学的な必然性はありません。

或るバクテリアの数が2時間で2倍になるとすると、三倍になるのには何時間かかるでしょうか。
t : 時間
N(t) : バクテリアの数
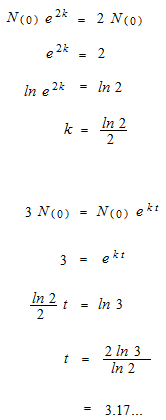
或るバクテリアが5分間に2%増殖しています。t分後には何倍になるでしょうか。