Continuously Compounded Interest
With logarithm, a calculation seems to be done with a very quick increase and its value would rise immediately to an astronomical number. But in fact, logarithm is actually used, as calculation of bank interest, rather with a very small value of rate and the curves are usually very slow and delicate.
The exponential growth or the exponential decrease are used just like a small amount of addition or subtraction.
y = logbx
x=by
First, as an easy example of logarithm, the calculation of a half-tone in twelve-tone equal temperament.
Twelve-tone equal temperament (i. e., “well tempered tuning”)
We are going to calculate the proportion of frequencies of a half-tone in twelve-tone equal temperament, called “well tempered”, using logarithm. The well-tempered tuning is not so good for very very low base notes nor very very high notes; Cf., “stretched tuning”. But for the midrange, the well tempered tuning gives the vibrations which are very pleasant to our ears. This “well tempered” tuning, which musicians of Bach’s time started employing, has trembling thirds and sixths, and also fourths and fifths in movement. The well tempered tuning assures the beauty of dodecaphony; Cf., Arnold Schönberg, Pierre Boulez
Now let’s calculate the proportion of a half-tone in twelve-tone equal temperament.
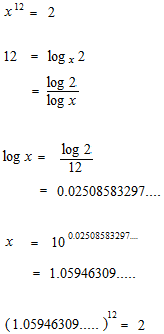
When you multiply the frequency of a note by 1.05946309…, you will get the note which is a half-note higher.
Bank interest
The calculation of bank interest may be not so interesting for you because you do not learn the math in order to calculate money. But this calculation of bank interest is very useful to understand the structure of exponential curves.
With understanding of calculation of bank interest, you will be able to apply it to other differential equation probrems. Without this understanding, learn to solve differential equations would have no interest.
In the following explanations, fictitious bank puts crazy interest. Also, after having deposited the proncipal, the account will not be touched any more.
It is called “continuous compound interest” , but in a real bank, they calculate interest on 365 days.
When the principal is 0 dollar, on whatever interest, balance stays 0 dollar.
Exponential curves never touch horizontal axis.
A certain amount of principal is needed to start. N0 is the amount of principal.
The variable of horizontal axis is t
At 0 % interest, the balance does not increase.
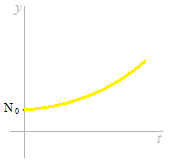
At low interest rate, the balance increases slowly.
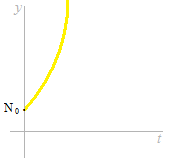
At a high interest rate, the balance increases rapidly.
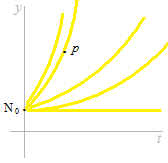
When N0 is fixed, there is only one curve which passes another point p.
Two points determine only one exponential curve.
A curve is determinated and its derivative too.
For instance, at point ( N0 , 0 ), only one slope of tangent line will be determinated.
If you know the amount of the principal and another amount of the balance on another day, you can calculate the rate of interest.
Namely, when two points are determinated, there is only one curve which passes these two points.
Philippe deposited 100,000 dollars of principal and forgot everything since. After a year, he discovered that his credit was 200,000 dollars. What was the rate of interest of this bank?
Suppose that 1/365 of annual interest is added every day.
rate of interest ; k
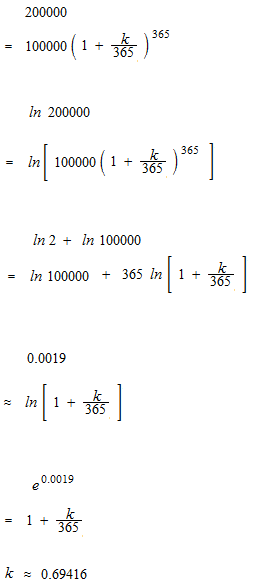
y = logbx
x = by
Using your calculator for constant values.
If 1/365 of annual interest is added every day, rate of interest 69.416% doubles the balance one year after.
Another bank. Even more generous.
At the rate of interest 100%, how much the principal 100,000 dollars becomes after a year?
1/365 of annual interest is added every day.
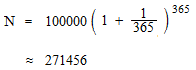
Being added every hour.
At the rate of interest 100%, how much the principal 100,000 dollars becomes after a year?
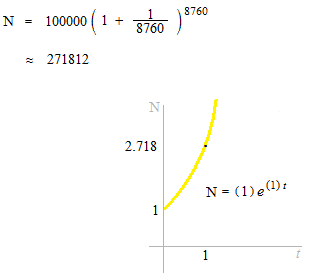
At a rate of annual interest 100% , being added at each infinitesimal time interval,
1 € will make € 2.718… dollars
This is the number e: the base of natural logarithms
Bank interest formula
N = N0 ek t
k rate of annual interest
t years
In a real bank, rate might be 2% as t . You put 0.02. Not 1.02.
Another bank.
Philippe deposited 1 dollars of principal and forgot everything since. After a year, he discovered that his credit was 2 dollars. What was the rate of interest of this bank?
Adding the interest at each infinitesimal time interval.
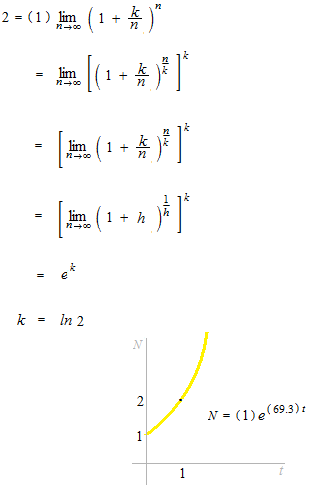
At rate of interest 69.3…%, the balance doubles after a year.
Only one curve passes points ( 0 , 1 ) , ( 1 , 2 ) .
Adding at each infinitesimal time interval, with rate of interest 100%, after one year, the balance becomes 2.718 times more, not 2 times. Then what does interst k mean?
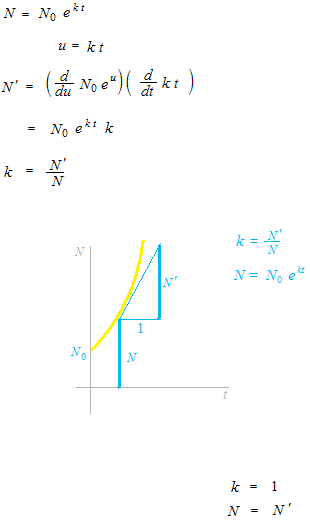
k is the proportion of N to N’ .
The 1 in this graph is the 1 in proportion to the tangent N’
It is not a value of k .
Show that these two equations say the same thing.
N’ = kN
N = N0 ek t
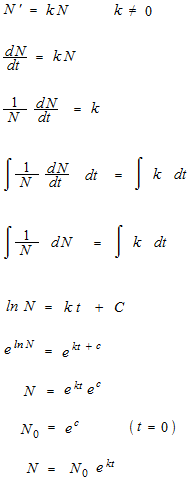
In reverse
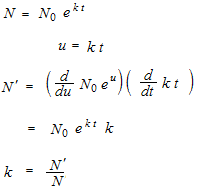
y'(t)=y(t)
y =
The answer would not be y =et
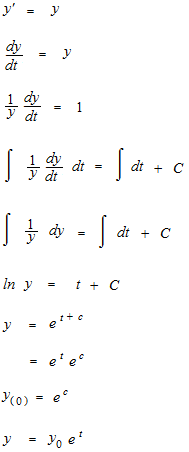
Sometimes it is difficult to assililate intuitively what the exponential function is. How about imagin that the decimal system were an exponential function with number of digits. Of course number of digit is integer, but just imagin as it were continuous t .
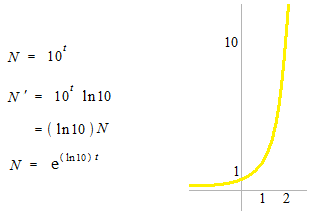
If there were a bank which makes 10 times after one year, the rate of interest would be
(100)(ln10) %.
The exponential function would be system of 2.718…
Initial condition N0 can be imagined as exponential function with initial condition 1 and instead of the unit 1 , you put N0 .
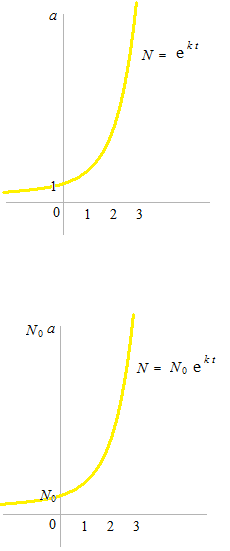
The exponential growth is a function whose proportion of the amount at a time and the inclination of the tangent at that time is constant.
