Intérêt continûment composé
Le logarithme semble se faire avec une très grande vitesse d’augmentation et la valeur pourrait monter tout de suite à un nombre astronomique. Mais, en fait, lorsque le logaritheme est utilisé au niveau pratique, c’est plutôt, comme dans le calcul d’intérêt de banque, avec un très petit taux et la courbe est très douce et lente. La croissance exponentielle et la décroissance exponentielle peuvent être utilisées presque comme des calculs réguliers d’additions et de soustractions.
y = logbx
x = by
Tout d’abord, comme un exemple facile de logarithme, voici la proportion d’un demi-tone dans le tempérament égal.
Le tempérament égal, dit bien tempéré
Nous allons calculer la proportion de fréquences dans le tempérament égal, dit “bien tempéré” en utilisant logarithme. Ce bien tempéré n’est pas tellement bien pour la partie très basse ni pour l’aigu, mais pour le registre médium le bien tempéré donne des timbres très agréables pour notre oreille. Ce tempérament “bien tempéré” que les musiciens de l’époque de Bach avaient commencé à employer a des tierces et des sixtes pétillants, des quartes et des quintes en mouvement. Ce bien tempéré serait l’origine aussi de la beauté du dodécaphonisme.
Calcul de la proportion d’un demi-tone “bien tempéré”.
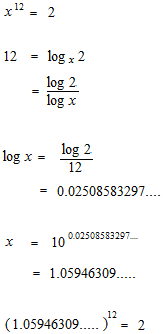
Dans le bien tempéré, la multiplication par 1.05946309… fait la note un demi-tone au-dessus.
Intérêt
Le calcul d’intérêt peut ne pas être très intéressant pour vous comme vous n’apprenez pas les maths pour compter de l’argent. Pourtant ce calcul de l’intérêt est très utile pour comprendre la structure de courbe exponentielle.
La compréhension de calcul d’intérêts vous permettra d’appliquer des équations différentielles à d’autres ploblèmes. Sans cette compréhension, apprendre à résoudre des équations n’aura pas d’intérêt.
Dans les exemples suivants, les taux d’intérêt seront unvraisemblables. En plus, après avoir déposé le principal, ce compte de dépôt ne sera plus touché.
Il s’agit de ” l’intérêt continûment composé “, mais, en fait, chez une banque réelle, l’intérêt est calculé par 365 jours.
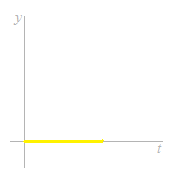
Lorsque le principal est de 0 € , quelque soit le taux de l’intérêt, le solde restra de 0 €. Une courbe exponentielle ne touche jamais l’axe horizontal.
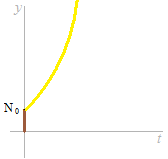
Un certain montant de principal est nécessaire.
N0 est le montant de principal.
La variable indépendante est t .
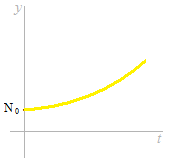
Au taux de 0 % d’intérêt, le solde restra inchangé.
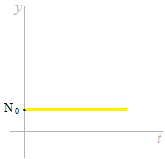
À un faible taux d’intérêt, le solde monte doucement. L’allure de l’augmentation d’augmentation est lente.
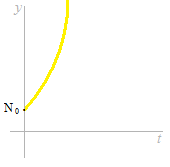
Au taux d’intérêt élevé, le solde monte rapidement. L’allure de l’augmentation d’augmentation est vite.
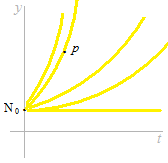
Lorsque un N0 est donné, il n’y a qu’un seul taux pour que la courbe passe par un autre point p .
Deux points déterminent une seule courbe expanentielle.
Une courbe est déterminée et sa dérivée aussi.
Par exemple, au point ( N0 , 0 ) , une seule inclinaison de ligne tangente sera détermimée.
Si l’on sait le montant du principal et le solde à un autre jour, on saura le taux de l’intérêt.
Philippe avait déposé 100,000 € de principal et tout oublié depuis. Au bout d’un an, il a rendu compte que son credit était de 200,000 €. Quel était le taux de l’intérêt de ce banque?
Supposons que 1 / 365 de l’intérêt annuel s’ajoute chaque jour.
l’intérêt annuel ; k
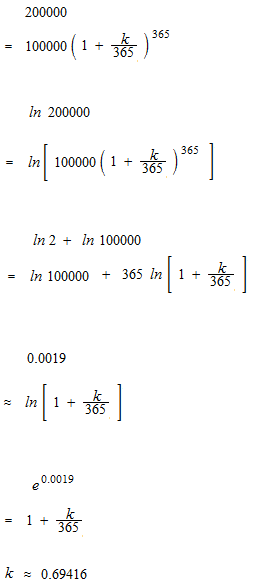
y = logbx
x = by
On utilise une calculatrice pour des constants.
Si 1 / 365 de l’intérêt annuel s’ajoute chaque jour, le taux de l’intérêt 69.416% double le solde après un an.
Une autre banque qui est encore plus généreux.
Au taux de l’intérêt 100% , le principal 100,000€, combien deviendra-t-il après un an?
1 / 365 de l’intérêt annuel s’ajoute chaque jour.
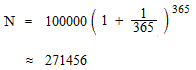
Si l’intérêt s’ajoute chaque heure.
Au taux de l’intérêt 100% , le principal 100,000€, combien deviendra-t-il après un an ?
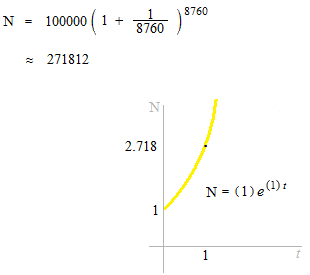
Au taux de l’intérêt annuel 100%, ajouté à chaque infiniment petit intervalle de temps, 1€ fera 2.718…€ après un an.
C’est le nombre e : la base du logarithme naturel.
Une seule courbe passera les points ( 0 , 1 ) , ( 1 , e ) .
La formule de l’intérêts de banque
N = N0 ek t
k taux de l’intérêt annuel
t ans
Chez une vrai banque, le taux serait à peu près 2%.
On met 0.02 comme t. Ne mettez pas
Une autre banque
Philippe avait déposé 1 € de principal et tout oublié depuis. Au bout d’un an, il a rendu compte que son credit était de 2 €. Quel était le taux de l’intérêt de ce banque?
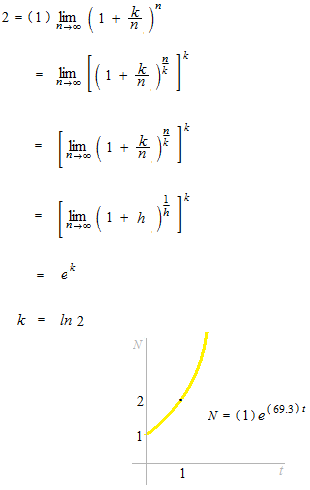
Le taux de l’intérêt 69.3…% double après un an.
Une seule courbe passera les points ( 0 , 1 ) , ( 1 , 2 ) .
Si k est à 100%, un an après, le solde sera multiplié par 2.718. Il ne sera pas multiplié par 2. Alors, que est-ce que c’est que cet intérêt k ?
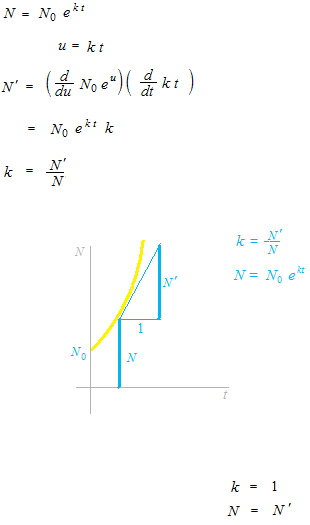
k est la proportion de N à N’ .
Le 1 dans ce graphique est le 1 par rapport à la tangente N’ .
Ce n’est pas une valeur de .
Pour N = N(t) k ≠ 0
Démonstration de ce que ces deux équations disent la même chose.
N’ = kN
N = N0 ek t
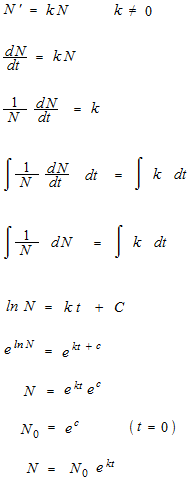
Dans le sens inverse
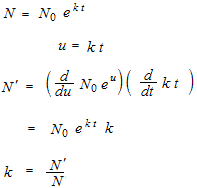
y'(t)=y(t)
y =
La réponse ne sera pas y = et
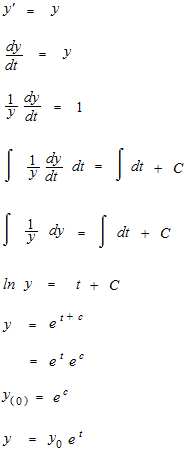
Juste pour assimiler intuitivement ce que c’est que la fonction exponentielle, on pourrait imaginer le système décimal avec le nombre de chiffres. Le nombre de chiffres est, bien sûr, un nombre entier. Cependant on peut imaginer comme si c’était continu t .
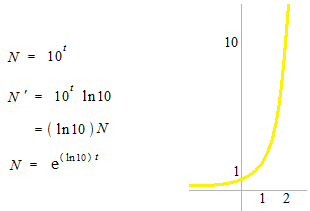
S’il y avait une banque qui fait 10 fois après un ans,
le taux d’intérêt serait (100)(ln10) % .
La fonction exponentielle serait le système de 2.718…
La condition initiale N0 peut être imaginée comme la même courbe que la fonction exponentielle à la condition initiale 1 et à la place de cette unité 1, on met N0 .

La croissance exponentielle est une fonction dont la proportion de la quantité à un moment et de l’inclinaison de la tangente au même moment est constante.
