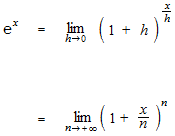Neperian number 2.718… (or Napier’s constant)
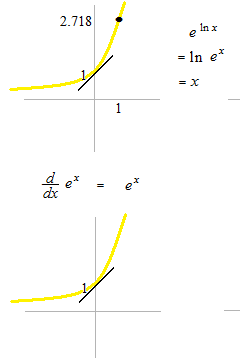
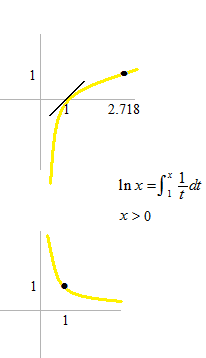
The slope of those tangent lines 1.
Exponential function and its derivative are the same functions.
Exponential function and natural logarithm function are inverse functions.
Natural logarithm function is défined by definite integral of the function y = 1/x .
These relations between the four function can be satisfied with the neperian number.
Between the derivative of exponential function and y = 1/x, there is no direct relation.
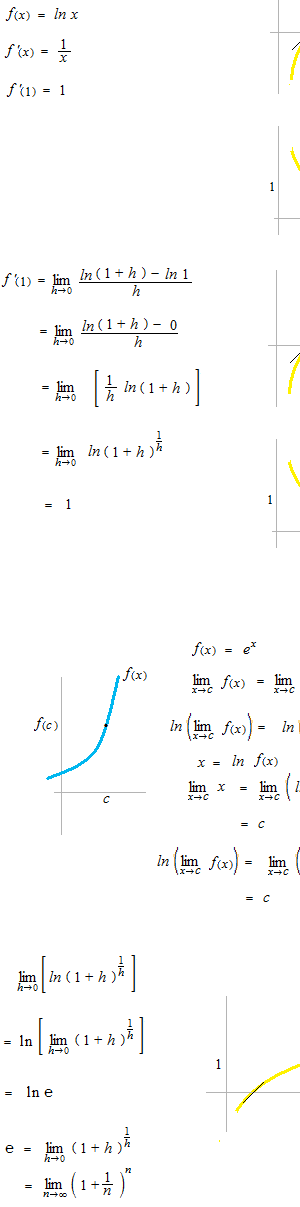
Differentiation of natural logarithm function.
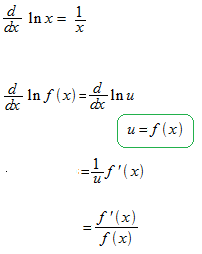
Absolute value after ln
![]()
Explanation ;
Normally after ln or log the value must be positive.
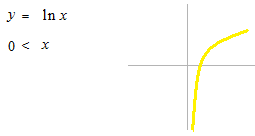
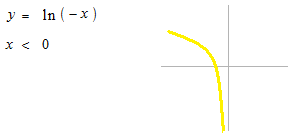
This one is also possible.
So, we write the two expressions together.
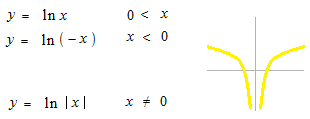
Differentiation
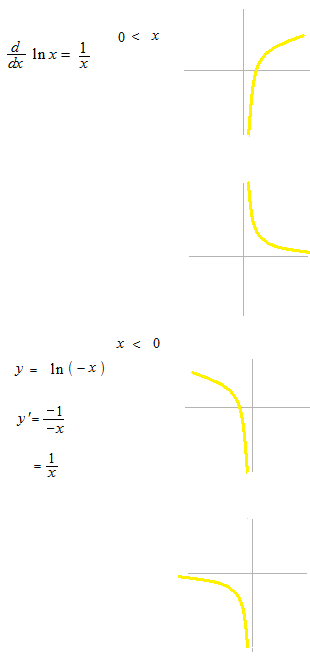
We write them together.
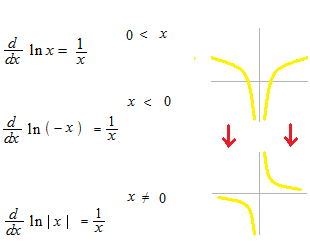
Indefinite integral
![]()
Example of differentiation of natural logarithm function.
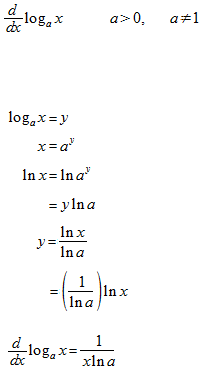
One more example of differentiation of natural logarithm function.
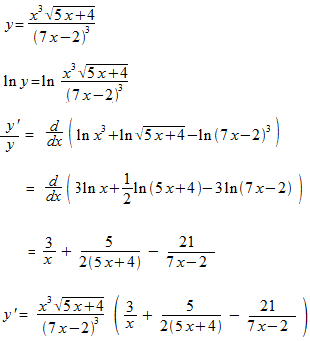
Differentiation of exponentiel function using the formula of differentiation of natural logarithm function.
First, la base is any real number.
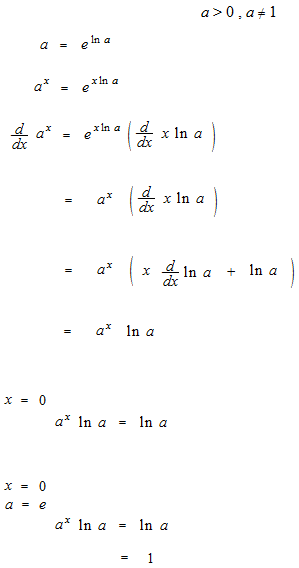
When base takes only e, differentiation is more simple.
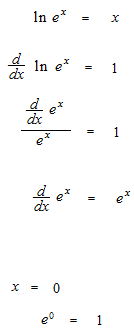
Example of differentiation of function exponential
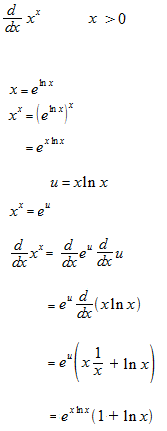
One more example of differentiation of function exponential.
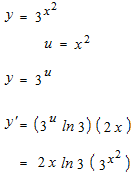
Integral of function exponential
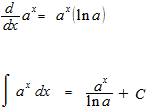
Example of integral of function exponential
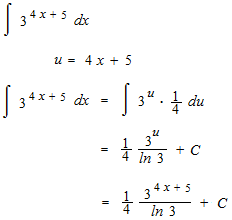
Calculation of the neperian number.
When x = 1, the limit of average rate of change, i.e. the slope of the tangent is 1.
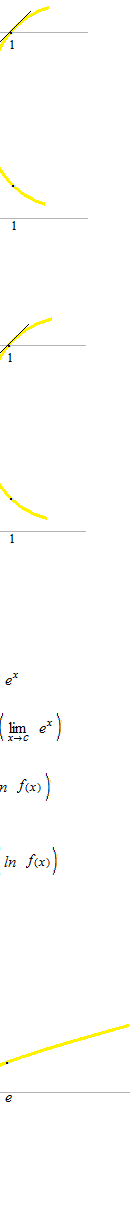
e can not be calculated directly with an equation.
n = 100 2.704814
n = 10 000 2.718146
n = 100 000 2.718268237
e = 2.718281828…….
If you use calculator of Windows, you can get the neperian number for exponential function, natural logarithm function, etc., in this way.
1
Inv
ln
=
2,7182818284590452353602874713527
For example
e3=20,085536923187667740928529654582
3
Inv
ln
=
20,085536923187667740928529654582
or
1
Inv
ln
x^y
3
=
20,085536923187667740928529654582
EXP button is just for floating point shift. This button works in the decimal system only.
0.88888888
EXP
3
=
888.88888
You roll dice and try to get a particular number, if you roll six times the probability is 100%. And the probability of losing all rolls is 33.5%.
With another game which is more difficult, for example one time on 60 of probability.
You try 60 times. The probability of losing all rolls is 33.5%
With much more difficult game, the probability is one on n times. You try times the probability of get one time is 100% , but at the same time, the probability of losing all is e-1.
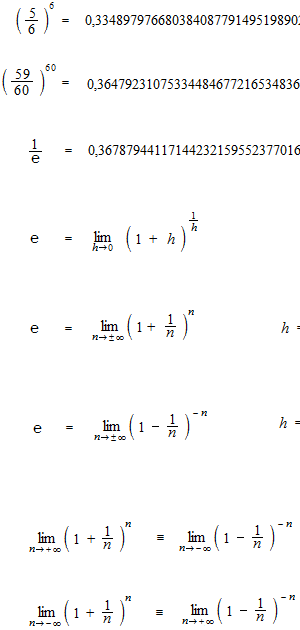
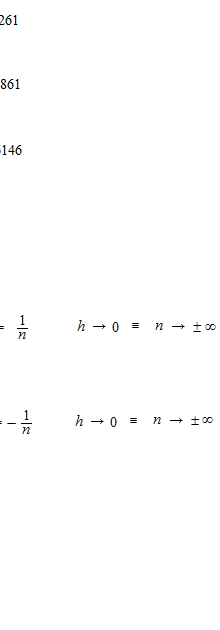
n is number which insrease partition. It is more reasonable when n is positive infinity.
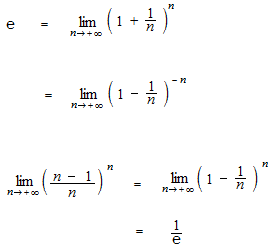
Definition of exponential function, using limit.