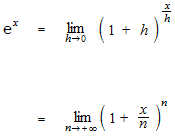ネイピア数 2.718…
「ネピア数」とも書きます。
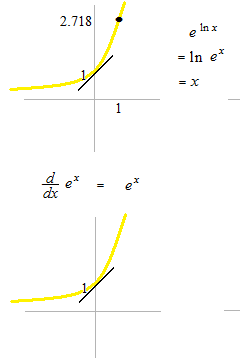
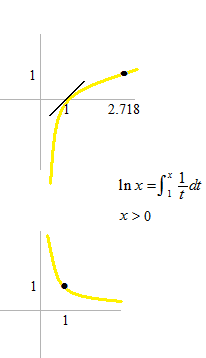
斜めの線は傾きは1です。
指数関数とその導関数が同じであること。
指数関数と自然対数関数は逆関数であること。
自然対数関数は反比例の関数の定積分によって定義されること。
四つのグラフのこれらの関係を満足させるのがネイピア数です。
ただし指数関数の導関数と反比例の関数は直接は関係がありません。
自然対数関数の微分
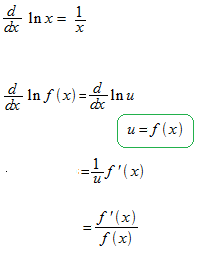
反比例の関数の不定積分には絶対値が付きます。
![]()
対数の計算では、log や ln の記号のあと、つまり何々乗された数はプラスのみを扱います。
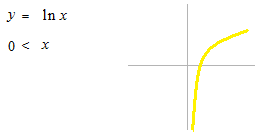
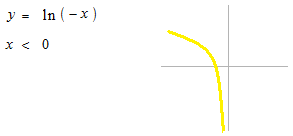
これも可能です。
まとめて書きます。
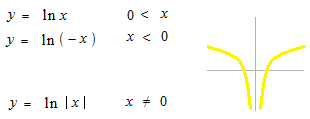
微分
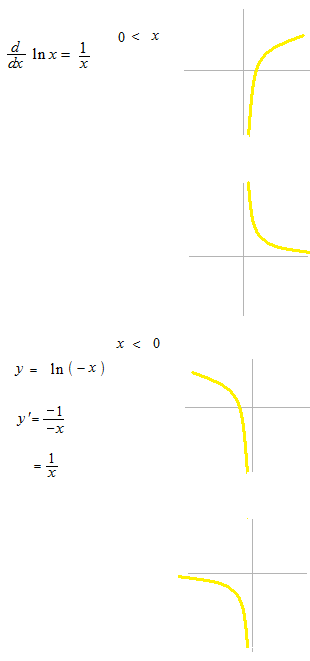
まとめて書きます。
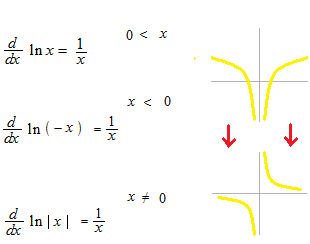
不定積分
![]()
自然対数関数の微分の例
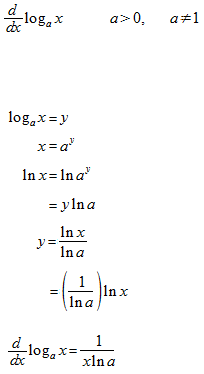
自然対数関数の微分の例
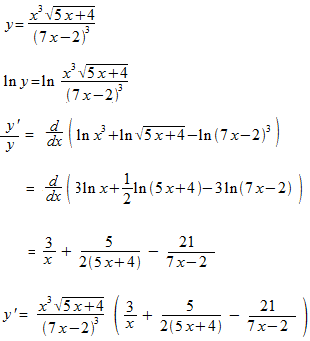
指数関数の微分
自然対数関数の微分の公式を使って指数関数を微分します。
まず底が任意の実数の場合
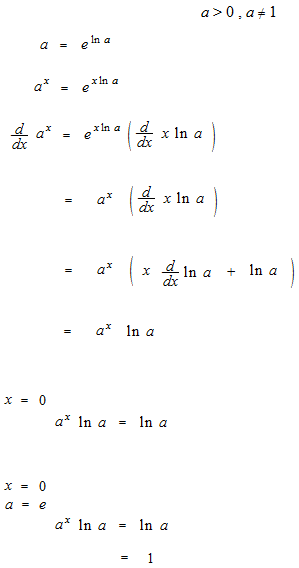
底が e の場合のみならば微分はもっと簡単にできます。
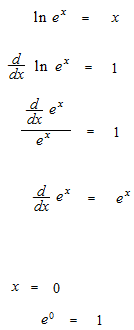
指数関数の微分の例
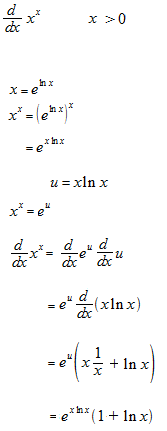
指数関数の微分の例
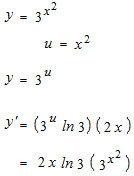
指数関数の積分
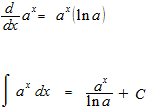
指数関数の積分の例
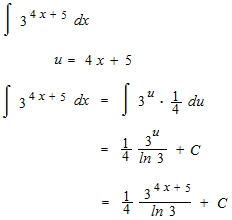
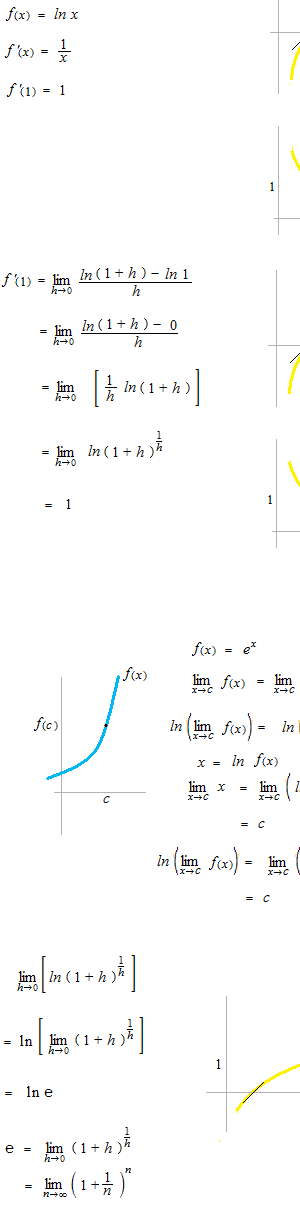
ネイピア数 e の値を計算します。 ネイピア数 e の x 乗の関数、指数関数、で ( 0 , 1 ) のとき傾きが 1 となる数がネイピア数 e です。ネイピア数 e の x 乗の指数関数を使ってネイピア数 e の計算の式を作ります。
x = 1 のとき、平均変化率の極限、つまり接線の傾きは 1 です。
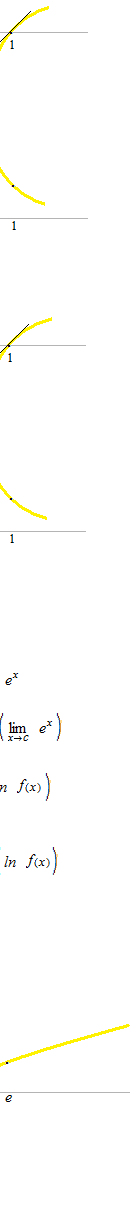
e は e の 1 乗というのは意味がないように見えますが、この 1 は曲線上の別の点に於ける傾きでもあります。
e は超越数なので2.718…という数は式からはすぐには出せません。
n = 100 2.704814
n = 10 000 2.718146
n = 100 000 2.718268237
e = 2.718281828…….
ウインドウズの電卓では指数関数、自然対数関数などでのネイピア数の値は下のようにボタンを押して出します。
1
Inv
ln
=
2,7182818284590452353602874713527
また、たとえば
e3=20,085536923187667740928529654582
3
Inv
ln
=
20,085536923187667740928529654582
あるいは
1
Inv
ln
x^y
3
=
20,085536923187667740928529654582
EXPというボタンは 10 の何乗というだけのものです。
0.88888888
EXP
3
=
888.88888
外れる確率
さいころの 1 の目を出そうとするとき、6 回ふると 1 回出る確率は 100% です。
1 回も出ない確率、すなわち 6 回とも他の 5 つの目のどれかが出る確率は33.5%です。
もっと確率の低いもの、たとえば 60 回に 1 回の確率のものを 60 回やって 1 回も当たらない、外れる確率確率は36.5%です。
非常に確率の低いものをその数だけやっても 1 回も当たらない、
外れる確率は e-1です。
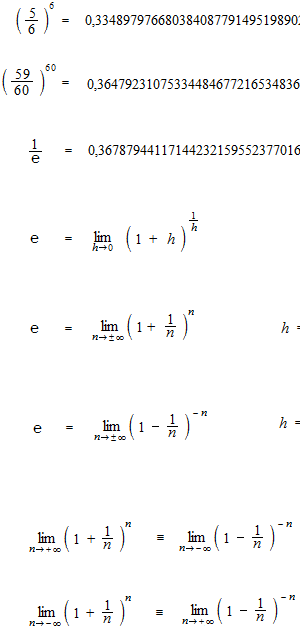
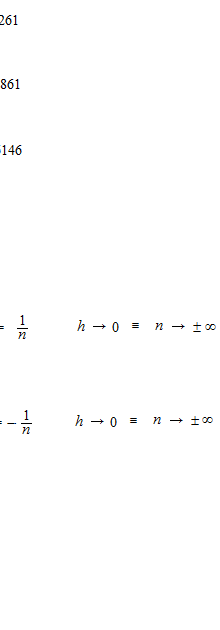
nは細かくしていく数ですので、プラス無限のほうをとります。
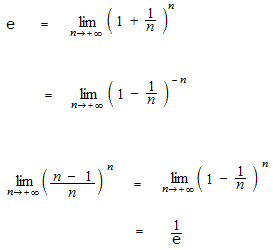
指数関数の定義
極限を用いると下のようになります。