La longueur d’une courbe , où la longueur d’arc.
C’est une révision de l’intégrale de Riemann.
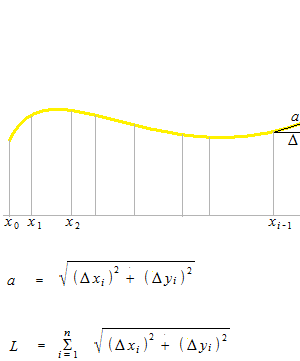
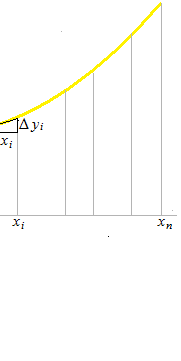
Il s’agit de la somme des valeurs de la longueur a.
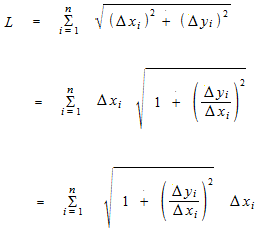
Il suffit de rendre infiniement petit. Mais comme une intégration de Riemann, il faut que cela soit la somme des rectangles sous une courbe.
La somme de quelle courbe?
On utilise le point c du théorème des accroissements finis de Lagrange.
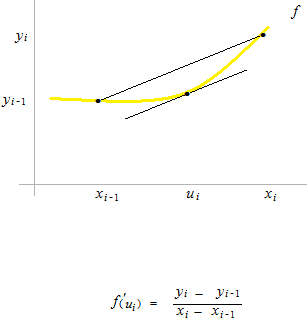
On désigne ui le point c du théorème des accroissements finis de Lagrange de chaque intervalle.
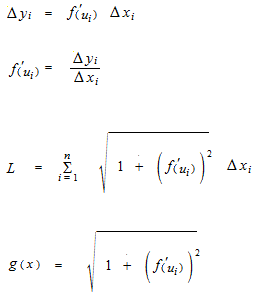
La hauteur de chaque rectangle est exprimée par g(x)
La limite de la somme de Riemann de g(x) sera la réponse.
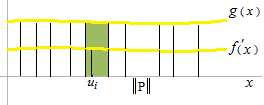
La somme de Riemann est une méthode des rectangles. L’intégrale de Riemann, c’est la limite de la somme de rectangles.
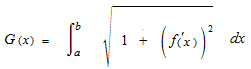
Il y avait quatre coubes.
Les coubes initiales du problme.
f(x)
g(x)
G(x)
