グラフの曲線の長さの積分
曲線の長さの積分を使ってリーマン積分の復習です。
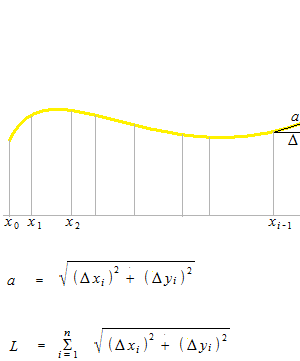
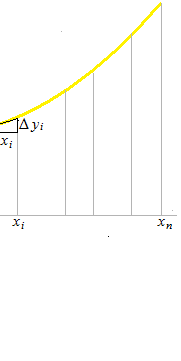
グラフの曲線をこまかく分けたときの aの部分の長さの総和です。
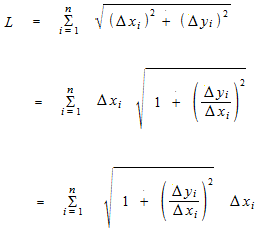
これを細かくすればよいのですが、リーマン和にするためにはグラフの長方形の和にしなくてはなりません。どのようなグラフのリーマン和でしょうか。
長方形の高さはラグランジュの平均値の定理の点cを使います。
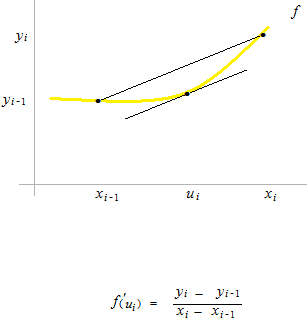
各長方形のラグランジュの平均値の定理の点cを ui としました。
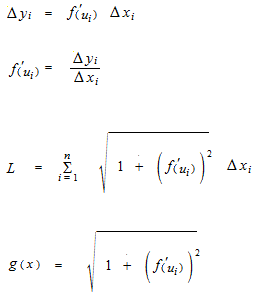
長方形の高さは g(x) で表されます。
g(x) のリーマン和の極限が答になります。
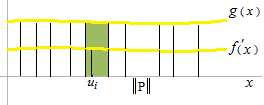
リーマン和は区分求積法のひとつです。リーマン積分は必ず長方形の和の極限として正しく理解しましょう。
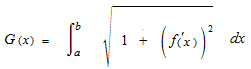
四つのグラフの曲線を使いました。
問の最初のグラフ
f(x)
g(x)
G(x)
