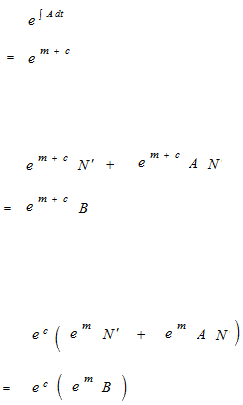Facteur intégrant; Constante d’intégration
Facteur intégrant pour équation différentielle linéaire du premier ordre.
Voici, un outils d’intégration qui s’appelle facteur intégrant.
On peut changer une équation différentielle
N ‘ + k N = A
qui contient une dérivée en une équation normale en multipliant deux côtés par ce facteur intégrant.
Avant d’expliquer ce que c’est que le facteur intégrant en détail, regardons ce qu’il pourra faire.
La page suivante de ce site vous présentera un problème de l’eau salée dans lequel il y aura une équation différentielle comme celle-ci.
Il faut répondre N(t) = ?
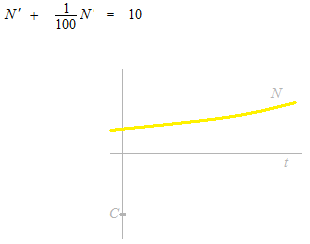
Si la question était N’ = 10, la réponse serait N = 10t + C
Mais il y a une pitite quantité en plus.
Si l’on multiplie les deux côtés de cette équation différentielle par e0.01t , on saura l’équation en forme normale, équation argebrique.
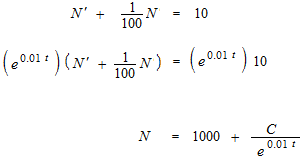
Cela sera éxpliqué plus bas et dans la page suivante. Très pratique.
Voici , l’éxplication.
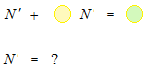
Un facteur intégrant sert à faire disparaître la dérivée d’une équation différentielle qui est en forme comme celle-ci, équation différentielle linéaire du premier ordre, et la rendre en forme normale, équation algébrique.
Ici, N(t) exprime la quantité de quelque chose qui est en augmenation.

Pour éliminer le terme qui est une dérivée, N’ , on pourrait faire une intégration les deux côtés de l’équation, mais cela ferait une intégration de N aussi. Comme on demande ce qui est N , on ferait une différentiation et cela ferait N ‘ encore une fois.
Il y a eu quelqu’un qui avait trouvé la maniére d’éliminer N ‘ en utilisant le fait que N’ peut être une partie du résultat d’une différentiation avec la règle de la chaîne.
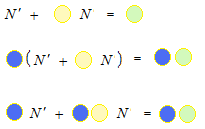
On multiplie les deux côtés par le facteur intégrant.
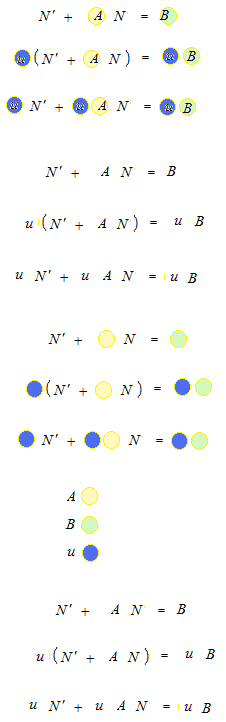
u est le faceur intégrant. u est un nombre qui satisfait que uB est le résultat d’une différentiation de uN.
On fait une différentiation de uB .

La régle de la chaîne.
Si u’ est uA , on aura N = …..
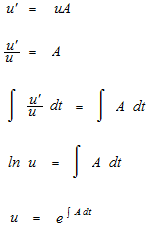
La constante d’intégration C de facteur intégrant n’est pas ajoutée par convention. Normalement la constante d’intégration C doit être toujours marquée comme la primitive ne sera pas déterminée après une intégration indéfinie. Mais la constante d’intégration de facteur intégrant peut être éliminée des deux côtés d’équation par anticipation.
La constante d’intégration C exprime n’est jamais déterminée arbitrairement. Il n’est pas possible de penser sans condition comme C = 0. Il n’est pas possible de penser comme il suffit d’avoir un seul facteur intégrant non plus. C’est essentiel de considérer que l’intégrale indéfinie n’est pas déterminée comme une quantité absolue.
C’est seulement pour la simplification en divisant deux côtés par eC que la constante d’intégration C de facteur intégrant ne sera pas écrite. C’est quelque chose de très simple.