Fundamental theorem of calculus….The beginning of indefinite integral
The integration meant essentially the limit operation of area calculation, limit of Riemann sum, Riemann integral, that is to say, definite integration that is done by the rectangle method.
The indefinite integration, which is nothing but the inverse operation of differentiation was not a true integration .
Nevertheless, almost always, definite integrations of functions are tedious or very often impossible, we use the indefinite integration as the integration.
Is this substitution always permitted ?
Fundamental theorem of analysis shows the close relationship between these two inverse operations. Differentiation and definite integration.
Fundamental theorem of analysis allows the substitution of the indefinite integration for Riemann integration.
First, let’s see a very simple example to understand the rough structure of the fundamental Theorem of analysis , then we will generalise it.
0 < f(x) continuous on [ a , b ]
We have four curves as models.
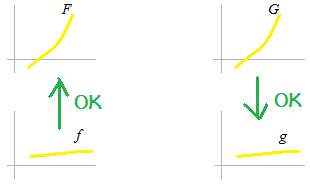
We are already OK with definite integration and differentiation.
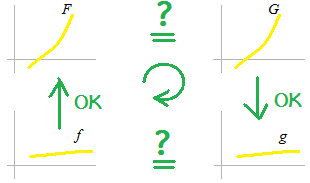
If…. then……
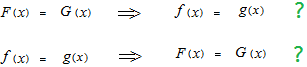
If such a relation is established, indefinite integral, that is only the inverse of derivative, can be used as a substitution of definite integral
This function F(x) is made by a definite integration. F(x) is determinated at point F(a) = 0 .Constant of integration C is out of quastion. The function F(x) is not an antiderivative.
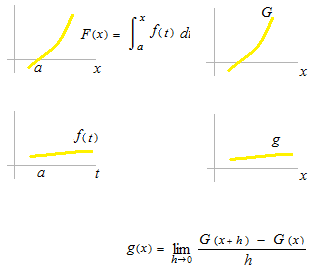
Dummy variable.
Dummy variable must be used here. When an integration determinntes no number value but makes a function, a dummy variable must be used. Or dummy variable is not used, therefore it is dummy variable.
Dummy variable is very important especially in the définition of
natural logarithm function y =ln x with the function y = 1/x.
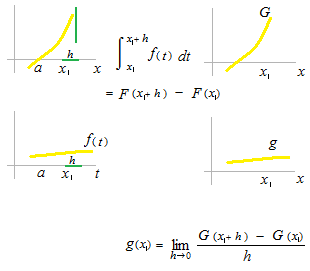
This definite integration is a Riemann integration. There is no discussion of the point to the height of each rectangular strip. Left nor right nor maximum nor minimum.
However small the largest interval ||P|| , the sum converges to a value.
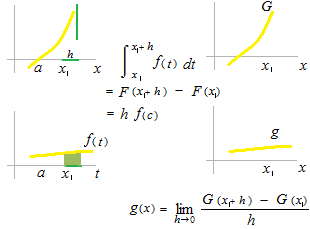
This c of f (c) is the c of the mean value theorem of integration. There must be more than one point c like this.
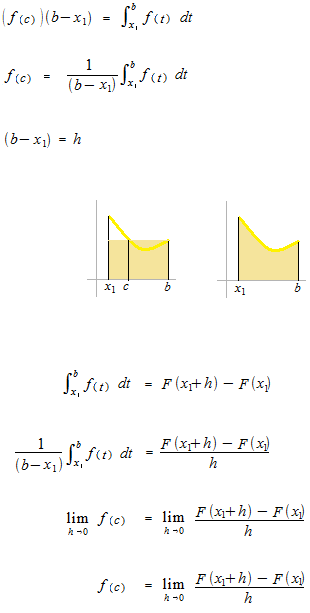
Fundamental theorem of calculus
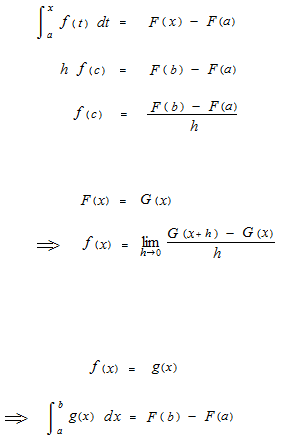
Fundamental theorem of calculus has showed the relation between definite integral and antiderivatives. After this fundamental theorem of calculus, now we can use antiderivatives in order to find a number value of definite integral operation. The function is called indefinite integral.
