Théorème fondamental de l’analyse.
Le commencement d’intégrale indéfinie
L’intégration désignait essentiellement l’opération de calculation d’aire par limite de la somme de Riemann, l’intégrale de Riemann, c’est-à-dire l’intégration définie qui est effectuée à la façon de méthode des rectangles.
L’intégration indéfinie, qui n’est que l’opération inverse de différentiation n’était pas une ‘intégration proprement dite.
Cependant, la pluspart des cas, comme l’intégration définie des fonctions sont fastidieuse ou très souvent impossible, on utilise l’intégration indéfinie comme opération d’intégration.
Est-ce que cette substitution est toujours permise ?
Thorème fondamental de l’analyse montre la relation étroite et inverse entre ces deux opérations. La différentiation et l’intégration définie.
Théorème fondamental de l’analyse permet la substitution de l’intégration indéfinie à l’intégration de Riemann.
0 < f(x) continue sur [ a , b ]
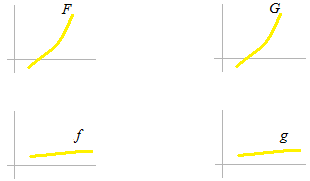
Voici quatre courbes comme maquettes.
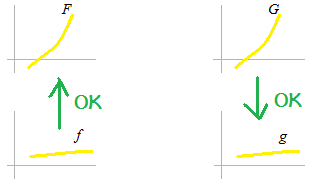
On est déjà d’accord avec l’intégration définie et la différentiation.
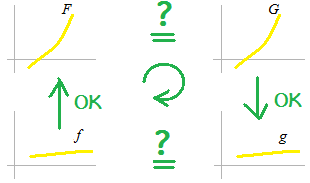
Si ….. alors …..
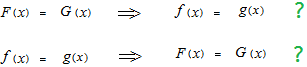
Si telle relation est établie, l’intégration indéfinie, qui n’est que l’inverse de dérivée, pourra utilisée à la place de l’intégration définie.
La fonction F(x) est faite par intégration définie. Elle est déterminée par le point F(a) = 0. Constante d’intégration C n’est aucunement concernée par cette opération. La fonction n’est F(x) pas une primitive.
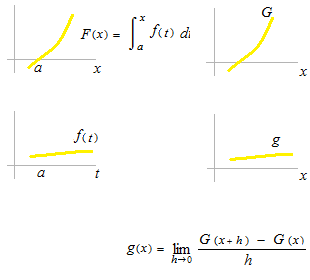
Dummy variable t
Il faut utiliser la dummy variable quand une intégration définie ne détermine pas un nombre mais produit une fonction.
La dummy variable est très importante quand la fonction logarithme naturelle,
y =ln x est faite de l’intégration définie de la fonction inverse, y = 1/x.
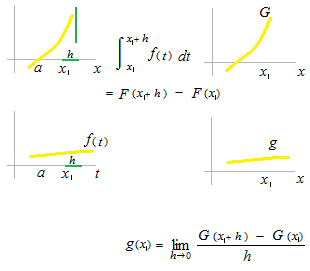
Cette intégration définie est une intégration de Riemann. Il n’y a pas de choix de point pour la hauteur des minces rectangles. Ni droite ni gauche ni minimum ni maximum. Quelle que soit la largeur du plus grand intervalle, la somme converge vers une valeur.
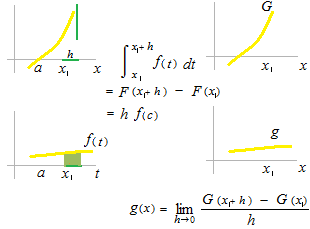
Ce c de f (c) est le c du théorème de la moyenne, il doit y avoir plus d’un c comme celui-ci.
Théorème de la moyenne.
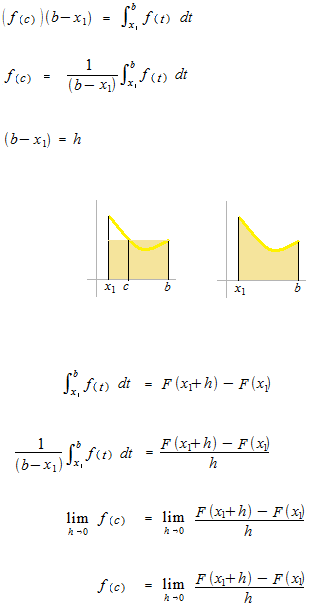
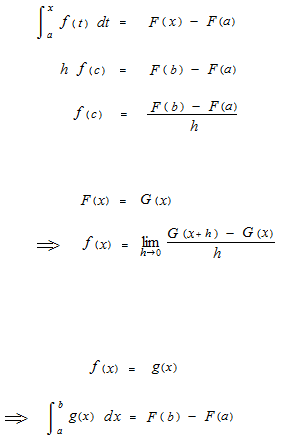
Le théorème fondamental de l’analyse montre la relation étroite entre l’intégration définie et la primitive. Grâce au théorème fondamental de l’analyse, désormais, nous somme permis d’utiliser les primitives pour chercher des valeurs de nombre de l’intégration définie. La fonction s’appelle l’intégrale indéfinie.
