微分積分の基本定理・・・・不定積分の始まり
本来、積分とはリーマン和の極限、リーマン積分による定積分、つまり区分求積法的に面積を求める作業のことです。微分の導関数の逆でしかない不定積分は、作業としては積分をしているとはいえません。ところが実際は関数をリーマン積分するのが困難なことが多く、不定積分をもって積分をすることが多くなります。この代用は常に許されるでしょうか。
微分積分の基本定理は微分とリーマン積分という二つの異なった作業が密接な関係で逆になっていることを示すものです。
微分積分の基本定理によって不定積分をリーマン積分に代用することが許されます。
0 < f(x) [ a , b ] で連続。
四つの関数のグラフをモデルとします。
定積分と微分は既に了解済みとします。
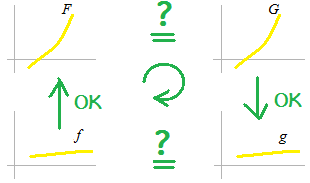
もし・・・ならば ・・・である。
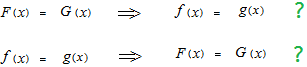
もし上のことがいえるのならば不定積分、導関数の単なる逆、を定積分の代用として使うことが常に許されます。
関数F(x)は F(a) = 0 と決められている定積分なので、積分定数Cはまったく関係ありません。
この関数は原始関数ではありません。
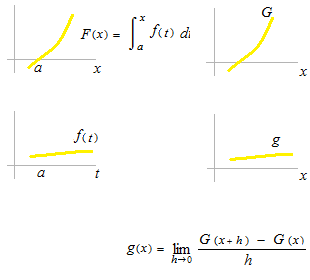
ダミー変数 t
ダミー変数は、定積分の結果から関数を作る場合に必ずを使います。 あるいは、使われないのでダミー変数と呼ばれるともいえるのですが。
ダミー変数を使った定積分は、
反比例の関数 y=1/xと
自然対数関数 y =ln x
の関係で重要ですので定積分の結果数値を出すのではなく関数を作る場合は必ず使います。
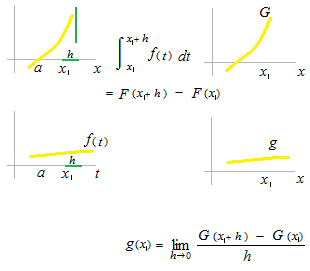
定積分はリーマン積分ですから、区分の細長い長方形の高さをどこでとるか、最大和、最小和ということは関係ありません。最も広い幅 ||P|| がどのようであっても或る値に収束しているということです。
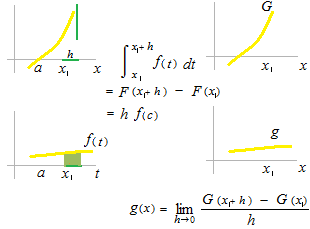
f(c)の cは積分の平均値の定理の cです。このような cが必ずひとつ以上あります。
積分の平均値の定理
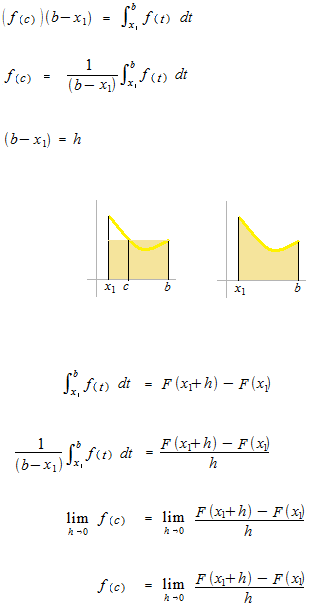
微分積分の基本定理は両辺をで割れるというところが決め手になります。
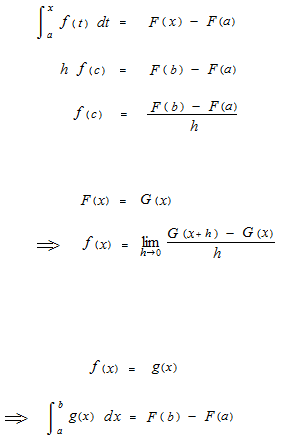
微分積分の基本定理は定積分と原始関数の密接な関係を示すものです。微分積分の基本定理によって定積分の数値の計算の容易な方法として原始関数を使うことができるようになります。この関数を不定積分と呼びます。
