Somme de Riemann
La méthode des rectangles → Somme de Riemann → Intégrale définie
Chercher l’aire sous la courbe de fonction positive et continue sur l’intervalle [ a , b ]
Somme de Riemann sert de pont entre la méthode des rectangles et de l’intégrale définie.
La méthode des rectangles.
Cette manière de calcul d’aire devrait exister depuis toujours. Pour l’aire sous la courbe, c’est lla somme des rectangles à base à longueur égale.
La somme de Riemann
La somme de Riemann est aussi une sorte de méthode des rectangles. Comme la somme de Riemann se fait pour aller être mise sous l’opération de limite, la hauteur de chaque rectangle est déterminée à n’importe quel point, u , dans la base. Ce n’est pas nécessairement au côté droit de rectangle ni au milieux.
Dans la différentiation, il a le point d’accroissements finis de Lagrange qui représente les points dans chaque largeur de bande, qui survit l’opération de limite et qui sera le paramètre pour la variable de la dérivée. Parce qu’une seule valeur peut être entrer dans la variable d’une fonction.
Dans la somme de Riemann, le choix de point pour hauteur de bande n’a pas dimportance. C’est le point du théorème de la moyenne qui survivra l’opération de limite. Mais ce n’est pas tout à fait nécessaire d’être moyenne.
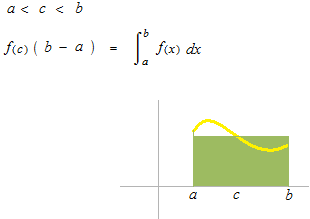
Il existe un tel point c.
La somme de Riamann n’exige pas que la largeur de chaque bande ne soit unique. La longeur ab ne peut pas être divisée par l’infinité. S’il paraît paradoxal de rendre la plus grande largeur ||P|| infiniment petite, alors on dit, comme epsilon-delta, que quelle que soit la petitesse de ||P|| .
Intégrale définie
C’est la limite de la somme de Riemann. Cela s’appelle égalemant l’intégrale de Riemann.
La méthode des rectangles
Cette manière de calcul d’aire devrait exister depuis toujours. Somme de Riemann est l’intermédiaire entre la méthode des rectangles et l’intégrale définie.
Nous allons chercher l’aire de la surface délimitée par la ligne d’une fonction positive et continue f(x), axe des xet les lignes x =a et x= b.
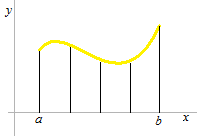
Nous divisons [ a , b ] en n parties égales.
La largeur de chaque rectangle est de Δx
b=a+n (Δx)
La hauteur de chaque rectangle est toujours au côté droit.
S’il y avait quelqu’un qui choisissait le côté gauche et à partir de i = 0 jusqu’à n−1, il serait fou.
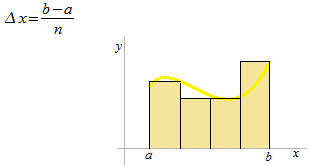
La hauteur H du i ème rectangle.
![]()
L’aire du i ème rectangle.
![]()
La somme de tous les rectangles S
![]()
Aire A
![]()
Trouvez l’aire.
y=4x
[ 0 , 10]
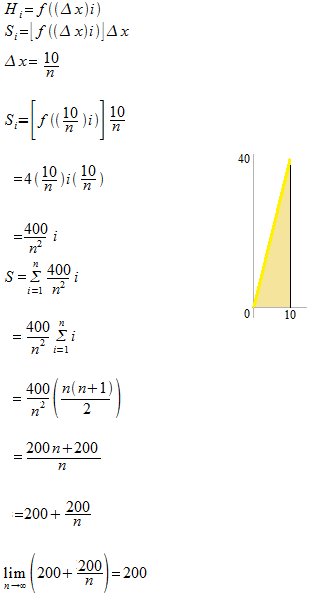
Trouvez l’aire.
y = − x2 +16
[ 0 , 4 ]
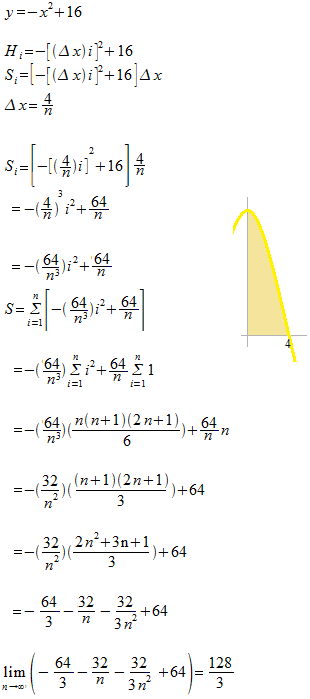
L’aire d’un demi-cercle.
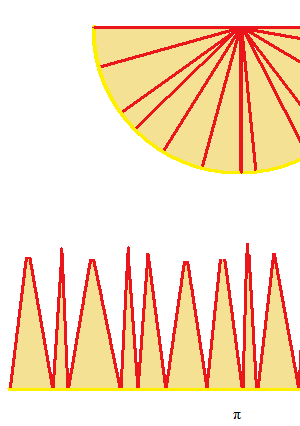
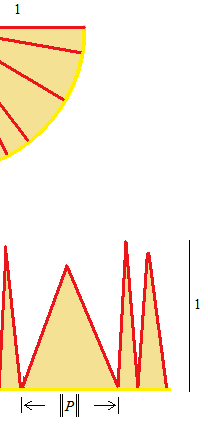
La figure semble être divisée en triangles isocèles, mais en fait, comme ce sont de petits secteurs circulaires, la ligne de la base n’est pas droite. Les hauteurs de ces secteurs circulaires ne sont pas égales.
Soit P, l’intervalle le plus large. La valeur de la largeur dep est représentée par ||P||.
La répartition en intervalles égals des secteurs circulaires serait plus facile. Mais, l’infini n’est pas un nombre. Nous ne pouvons pas diviser π par l’infini pour avoir une échelle égale. Nous ne divisons pas π par l’infini, mais, à la place de cela, nous disons “quelle que soit la largeur du plus grand intervalle”. Cela veut dire “dans tous les cas”, pour éviter ces adjectifs ambigus, petit et grand.
Calculer l’aire de chaque secteur ciculaire est très difficile à réaliser. Donc, nous lions tous les sommets.Cela fait une ligne extrêmement complex mais c’est une fonction. Soit f (x) . C’est une véritable fonction, car il n’y a qu’une seule valeur d’ y pour une valeur d’ x .
Maintenant, la largeur de chaque intervalle est infiniment petit. La irrégularité de la courbe sera compréssée.
Toutes les hauteurs convergent à 1 et nous avons un grand rectangle qui a π de superficie. Ce grand rectangle peut être considéré comme une collection de rectangles infiniment minces. Dans la figure ci-dessous, trois rectangles minces sont exprimés gros pour mieux montrer.
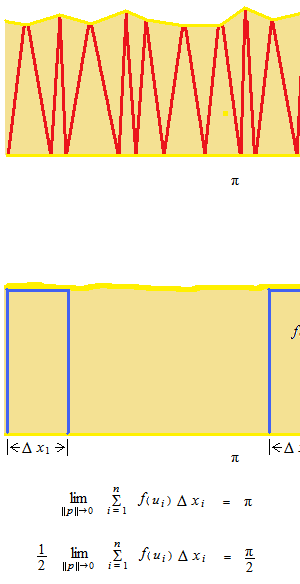
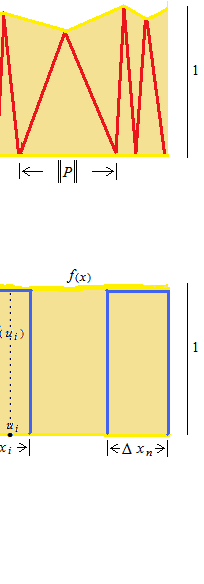
Ces expressions se lisent;
Quelle que soit la valeur du plus grand intervalle ||P|| , cela veut dire, la plus grande largeur s’approchera infiniment de 0.
n est le nomble de rectangles trés minces.
Δ xest la largeur de chaque intervalle.
N’importe quel point à l’intérieur de chaque intervalle peut être nommé u.
La hauteur de chaque rectangle est de f(u) .
Δ x , u , f(u) du iième rectangle sont Δ xi , ui , f(ui)
Le total d’aire, à partir du premier rectangle mince jusqu’au n ième, doit être de π . L’aire du demi-cercle est de π divisé par 2.
Somme de Riemann est une sorte de méthode des rectangles. Mais somme de Riemann est présupposée qu’elle soit calculée avec la limite. La somme de Riemann ne contient pas des choses qui sont incompatibles avec l’opération de la limite.
Comme la somme de Riemann sera toujours calculée avec la limite, le choix de hauteur n’a pas de place pour être discuté. La largeur de rectangle sera infiniement étroite, donc il ne sera plus de question en ce qui concerne le choix de hauteur.
Comme tous les rectangle auront la largeur infiniment petite, chez la somme de Riemann, l’égalité de largeur est exclue.
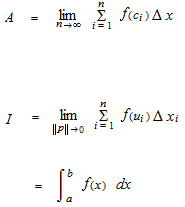
A est la formule de la méthode des rectangles.
I est la formule de la somme de Riemann avec la limite, donc intégrale définie. Cela s’appelle aussi, l’intégrale de Riemann .
||p|| est la plus grande largeur des rectangles.
Intégration définie.
Intégrale définie est la limite de la somme de Riemann. L’intégrale définie est tout à fait indépendante de la différentiation.
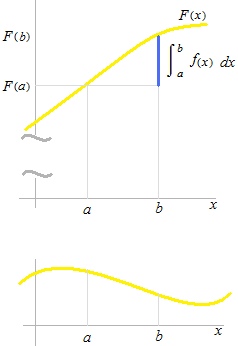
L’aire de la surface délimitée sous la courbe de f(x). [ a , b ]
Cela est aussi la différence de F(a) et F(b)
Si l’on suppose que dx,dt et dysoient des valeurs de longueur, on pourra imaginer de l’intégration comme ceci.
On peut dire que dx, qui est le dénominateur de proportion, redevient, Δxqui est la valeur de longueur.
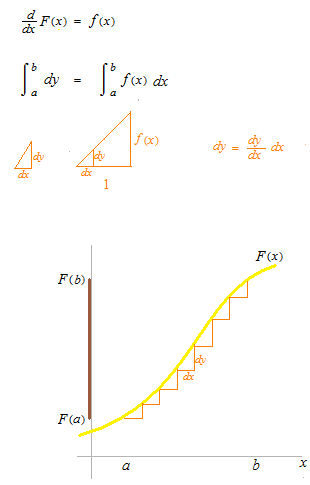
Le résultat d’une intégration est un nombre.
L’intégrale est un nombre.
Il n’y en a pas de fonction F(x) qui soit le résultat d’une intégration définie sur une fonction f(x).
[ a , b ]
Mais il peut y avoir une fonction I(x) comme une fonction de la différence entre F(a) et F(x)

Ce moyen d’une intégrationest utilisé pour obtenirla fonctionlogarithme naturel.
y = ln x à partir de y = 1/x .
