リーマン和 リーマン積分
区分求積法 → リーマン和 → 定積分(リーマン積分)
連続で常に正であるような関数 f(x)の曲線、x 軸、直線 x = a 、直線 x = b 囲まれた部分の面積を求めます。
リーマン和は、区分求積法と定積分の橋渡しです。
区分求積法
面積の計算として、区分求積法は大昔からあったはずです。グラフで考える場合は、縦に並べた均等な幅の帯の面積の合計です。
リーマン和
リーマン和も区分求積法なのですが、リーマン和を無限に細かくすると定積分になるということを前提にしているので、リーマン和では帯の高さをどこでとるかは問題とはされません。
微分の場合は、ラグランジュの平均値の定理があって、どんなに細かくしても (どのような幅にしてもといったほうがエプシロンデルタ論法的ですが) 、どんなに細かくしても必ず傾きを代表する点があり、その点が、無限に細くしていく幅の間に最後まである、だから極限値の際の x として一点となり、導関数のパラメーターともなります。二点では導関数の x に入れようがありませんから。
積分の方法として、リーマン和では高さの点は帯の幅のうちのどの点でもよいということになっています。幅を無限に狭めてもなお最後まで残る点としては、「積分の平均値の定理」の点ということになりますが、平均値である必要はありません。
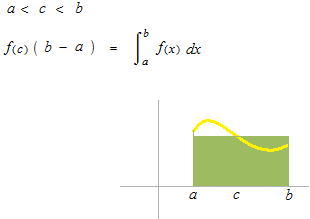
このような点 c が必ずひとつはある。また、リーマン和では帯の幅は均等である必要がありません。
最も広い帯の幅が無限に狭くなったときを前提にしているので、リーマン和では幅は問題とされません。長さ ab を無限で割ることはできません。最も広い帯の幅を無限に狭くするというのは矛盾があるようですが、最も広い帯の幅がどのような値であってもとエプシロンデルタ論法的にいえばいいわけです。
定積分
リーマン和の極限が定積分です。リーマン積分ともいいます。
区分求積法
まず、大昔からあった区分求積法 の考え方。
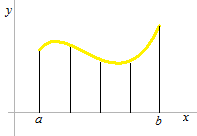
区分求積法では、 区間 [ a , b ] を n等分します。区分求積法の帯の幅はすべて同じ幅 Δ xとします。
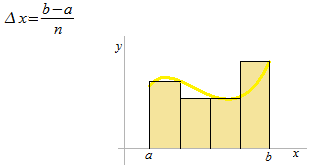
それぞれの帯の必ず右側を高さとします。左側を高さにして i= 0から n − 1までとする人の人格が疑われます。
i番目の帯の高さ Hi
![]()
i 番目の帯の面積 Ai
![]()
全ての帯の合計 S
![]()
分割の数を無限に増やすと細かく面積が計算できます。
面積 A
![]()
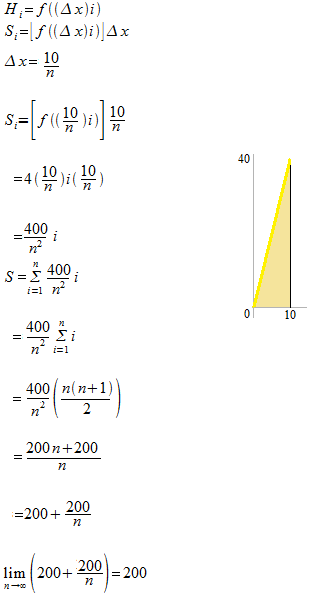
区分求積法の例 1
グラフのしたの面積を求めます。
y= 4 x
[ 0 , 10]
区分求積法の例 2
y = − x2 +16
[ 0 , 4 ]
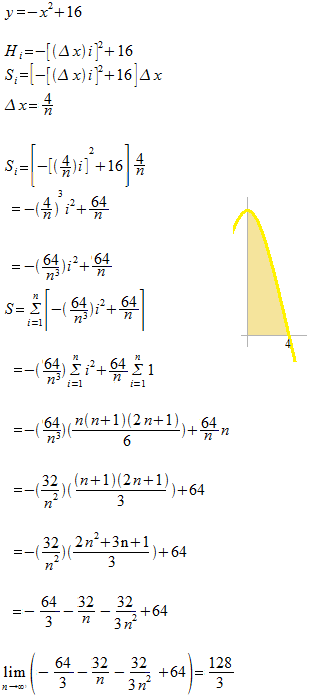
リーマン和
半円の面積を出します。
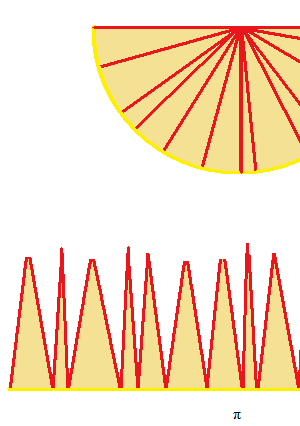
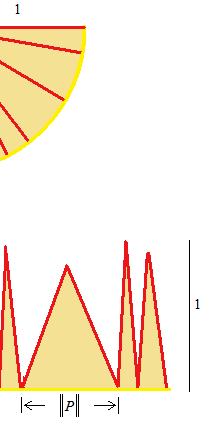
図では半円を沢山の二等辺三角形に分割したように見えますが、沢山の扇形です。高さは不揃いになります。最も広い幅の区間を P として、その幅の長さを ||P|| と表します。均等に分割した方が簡単ではないかと思われるでしょうが、これから無限に細かくしていくのですから、均等ということに意味がなくなります。無限は数値ではないので、 π を無限で均等に割って幅をすべて無限分の1にするという式はありません。ひとつひとつの扇形の面積を出すのは難しいので、頂点をすべて結んでしまいます。できた線は、折れ線グラフになります。極度に複雑なグラフですが立派なひとつの関数のグラフです。幅を非常に細かくしていきます。するとほとんど直線に近い線になります。すべての扇形が、高さが1の細い二等辺三角形になっていきます。すべての高さが1に近くなっていきます。できた大きな長方形を、とても細い幅の長方形の集まりとします。ただし、下の図ではとても細いはずの長方形の幅を広く描いてあります。
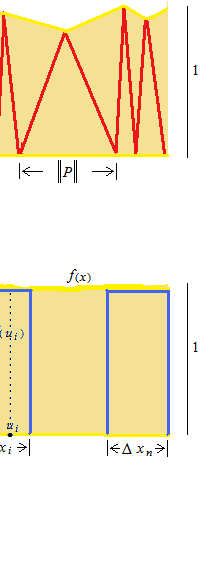
この式の読み方。
最も広い幅がどのように細かくてもよいという意味で、||P|| を無限に 0 に近づけます。全部で n本の細い長方形があります。長方形の幅を Δx とします。各長方形の幅の内側のどこでもよい点を uとします。長方形の高さはf(u)です。i番目の、幅、点u、高さはそれぞれΔxi, ui, f(ui) です。
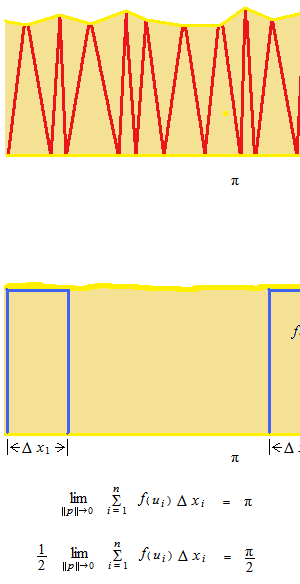
幅 Δx 、高さ f(u) の長方形の面積を1 番から n 番まで全部合計すると πになります。
半円の面積は二等辺三角形の合計なので 2で割ります。リーマン和の幅を無限に細かくしたものが、定積分です。リーマン積分とも呼びます。リーマン和は区分求積法の不必要な要素をはぶいたものといえます。区分求積法をいきなり無限に細かくしても結果は同じです。定積分の式は、ここからここまでを積分するというように関数そのものを使って表されます。定積分は帯の幅という意味で dx を使っていますが微分からの方向からは独立しているところに定積分の素晴らしさがあります。
積分の平均値の定理も定積分の面積を前提にしています。
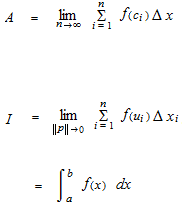
A は区分求積法の式
I はリーマン和を無限に細かくしたリーマン積分、つまり定積分の式です。||p|| はリーマン和の無数の帯のうちで最も広い帯の幅です。uiは幅の中ならばどこでもよい点です。
不定積分のどこからどこまでとして、Cをつけないのが定積分というのは違います。不定積分は導関数の逆。定積分は区分求積法やリーマン和の極限値への収束です。ところが関数をシグマを使った式から極限値を求めるのが困難な場合が多いので、通常不定積分の差を積分計算の答とします。
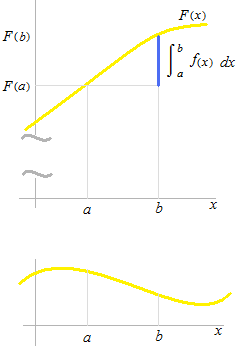
連続した正の関数 f(x)を aから bまで定積分すると関数f(x)のグラフ、x 軸、直線 x = a、直線 x = bに囲まれた部分の面積が得られます。また、別の言い方をすれば、関数 f(x)を或る関数 F(x)の導関数としたときの fa)と f(b) の差の値が出ます。
dx, dt, dyなどを長さとみなして考えても積分ができます。比率の分母 dxをもとの細かな Δxに戻したともいえます。
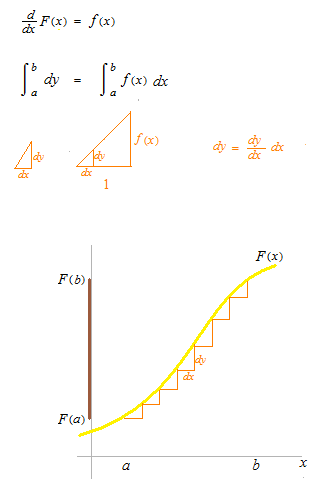
定積分で得られる答は、ひとつの数値です。関数ではありません。関数 f を a から bまで定積分した値の出るような関数 I(x)というものはありません。関数 f(t) を関数 F(x)の導関数としたときの F(a)F(x)の差の関数ならあります。
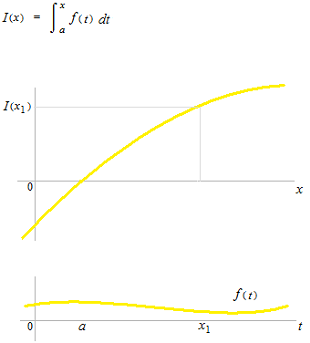
これは自然対数関数を反比例の式から作るときに使われます。
y= ln x
y= 1/x
どこかのサイトで「g・・・・・yさん」の疑問を拝見致しました。私のサイトをごらんいただきありがとうございます。「一番広い幅と一番狭い幅の区間が極端に違う時、一番狭い幅が0に限りなく近くなったら、一番広い幅はもう小さくなれないのではないか」という疑問。一番狭い幅が0に限りなく近くなっても、一番広い幅もまた0に限りなく近くなります。どの部分を見ても0に近くなるという意味の「表現方法」だからです。エプシロンデルタ論法というものがあって、それ以後、「すごく小さくする」といったような形容詞を使うのは数学的な論証らしくないことに対し、「どの部分を見ても、或る値の範囲に必ず入る」という言い方が始まりました。一番広い幅が0に近くなったら他の部分のどの幅を見ても0に近くなるという言い方です。積分は限りなく正解に近い近似値です。みかんの輪切りのような扇型はどれだけ鋭角にしてもやはり扇型です。ぐちゃぐちゃした細かい部分を「限りなく正解に近い近似値は正解に等しい」という「表現」のなかに押しつぶしてしまいます。別の見方をすれば、微積分とは「或るひとつの量を無限で割ったときも 0 にはならないからこそ、0 に限りなく近い近似値の中で様々な式が可能になる」ことを使った計算であるとも言えます。テイラー展開が近似値の式ですから、オイラーの等式も近似値の式です。正解に向かって「収束している」という考え方です。
