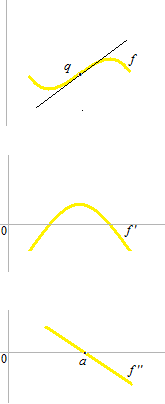
ラグランジュ 平均値の定理
平均値の定理は定理なので、あたりまえのような内容に見えますが、導関数がプラスのとき原始関数が右上がりになるというようなことの証明に使います。
[ a, b ] でf'(x) > 0 のとき、 f(x)は常に増大していることを証明します。
[ a, b ] で、ふたつの任意の xの値を x1と x2 とします。 .
x1 < x2
( x2 − x1 ) f ‘( c) = f (x2)− f(x1)
このような c が必ずひとつ以上あるはずである。平均値の定理
( x2 − x1 ) > 0
f'(c) > 0
したがって
f(x2) − f(x1) > 0
平均値の定理はロルの定理をもとにしています。
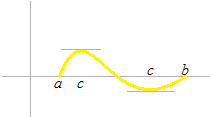
ロルの定理
a < b
g(a) =g(b )
であるとき、少なくともつぎのような c がひとつ以上あるはずである。
a ≤ c ≤ b
g'(c) = 0
平均値の定理
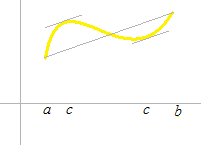
少なくともつぎのような c がひとつはあるはずである。
x1 ≤ c ≤ x2
![]()
理由を、まず、一次関数で見ます。
f(x)と g(x) は一次関数です。
g(x)を f(x)を使って表します。
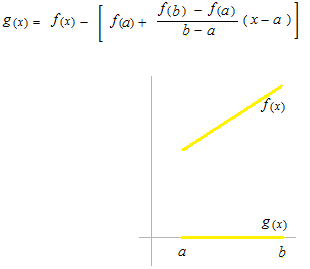
今度は f(x) は一次関数とはかぎりませんが、式は同じです。
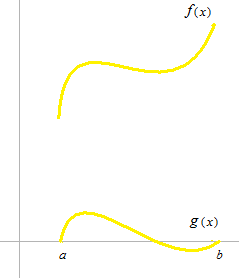
f(x)からロルの定理的なg(x)を定義します。
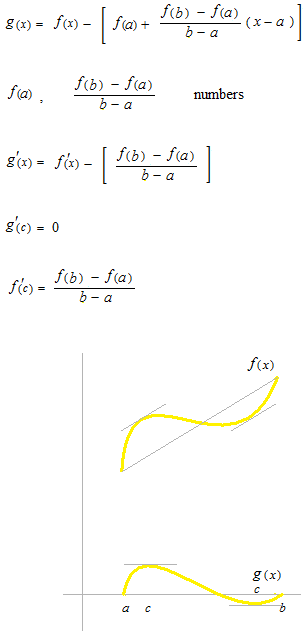
[ a , b] で f”(x) > 0のとき、 f(x) は常に反り上がっている
凸関数であることを証明します。

まず f(x) 上の点 ( p, f(p) )での接線の方程式。
y= f(p) + f'(p) ( x- p)
再び平均値の定理を使います。
p< c < x
どのような cがあるのでしょうか。
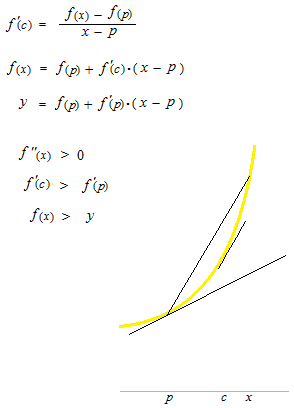
図の点 qのように凸関数と凹関数の切り替わる点を変曲点といいます。
点 qに於ける接線。
( y − f(a) ) =f'(a) ( x − a)