La fonction composée; la règle de la chaîne.
Utilités des fonctions composées.
1. Factorisation.
2. Règle de la chaîne dans des différentiations. Application sur des formules.
3. Substitution dans des intégrations. Application sur des formules.
4. Réciprocité de fonction ln et de fonction exponentielle.
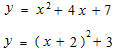
Une équation avec des parenthèses est déjà une sorte de fonction composée. Voir distributivité, associativité, commutativité. Cela facilite des opérations. Au niveau différentiel, dy dx , l’unité d’échelle des coordonnées de la fonction extérieure change de mesure.
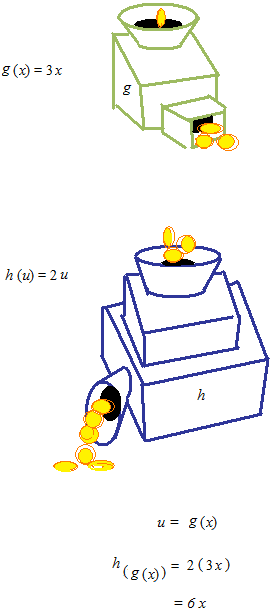
Voici, une machine qui multipliera par trois la monnaie qu’on a mise. Cette machine sera nommée g .
Il y a une autre machine, h, qui multipliera la monnaie par deux. Si l’on met la monnaie qui est sortie de la machine g directement dans la machine h .
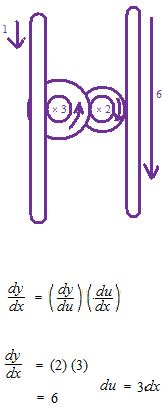
Visualisation de la règle de la chaîne. Imaginez ce que c’est que la règle de la chaîne en regardant cette figure. La règle de la chaîne est le produit des dérivées des fonctions. Différentiation avec la règle de la chaîne.
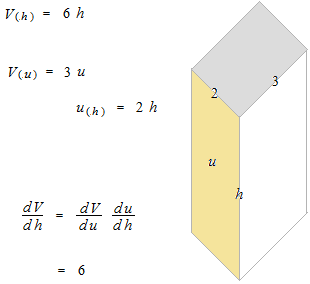
Si la variable est la hauteur d’un volume.
Chacun de ces deux grands triangles rectangles est à part entiére. Ils sont indépendants.
La tangente est la proportion de la hauteur de triangle rectangle à la base “1” .
Chacun a son “1” à valeur différente.
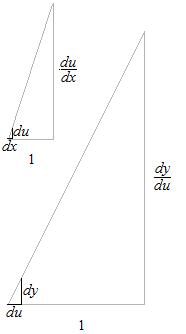
La fonction intérieure détermine des echelles des coodonnées de la fonction extérieure.
Entre ces deux fonctions g(x) , h(u), on peut penser qu’il y a une différence au niveau de largeur de graduation. Si, d’abord, on a une fonction et la change en une fonction composée de deux fonctions, on dénombrera trois fonctions en tout. Ici, pour un moment, seul la composition de deux fonctions sera mentionnée.
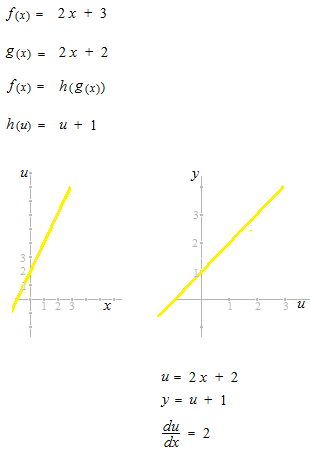
Regardez ces graphiques.
Comme du est deux fois plus long que dx, l’unité “1” des coordonnées u – y est deux fois plus longue que celle des x – u.
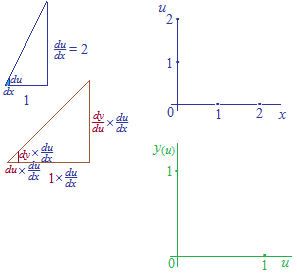
Les graphiques de deux fonctions d’une fonction composée sont chacun sur les coordonnées à échelles différentes de longueur d’unité “1” .
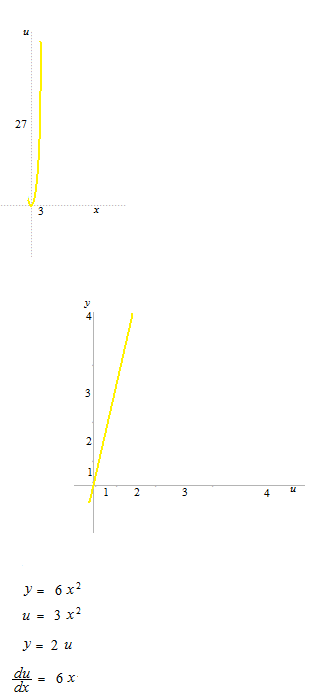
Les échelles des coordonnées de la fonction éxtérieure ne seront pas régulières sauf quand fonction intérieure est linéaire.
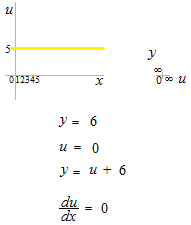
Si l’on fait une fonction composée à partir d’une fonction constante avec la règle de la chaîne, on aura le dénominateur du = 0 .
