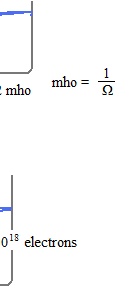加速度とは何か

このページの趣旨。
簡単なことを複雑に説明するのは、けっして好ましいことではないのであるが、本質的に複雑なものを簡単に説明してしまうのもまた誤りのもととなる場合が少なからずあるのではないだろうか。ニュートン自身は彼の著作が一般人に広く読まれることを意図し、彼の力学を微分を使って説明することはしなかった。一次関数のグラフ、すなわち直線グラフの微分は単純な割り算と同じ結果となり、したがって微分をまだ勉強していない子供たちには加速度の概念が割り算で説明されていることが多いのであるが、はたして本当に割り算による説明のほうが微分による説明よりも理解しやすいといえるのであろうか。加速度の本質が直感的には理解できないものであるならば、子供たちに割り算で説明されるべきではない。加速度の説明は微分の説明に他ならない。
注意 1.
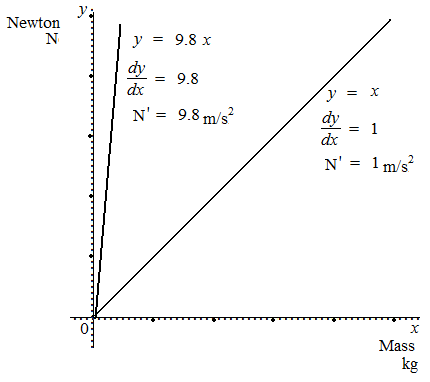
時間、移動距離、速度、加速度に関する理解のためには、グラフは必ず横軸が秒、縦軸がメートルであり、1秒と1メートルが正方形になるような方眼に描かれる必要がある。それ以外の方眼に描かれたグラフは、たとえ微積分を知らない子供たちのための説明であっても、関数のグラフの傾きに関する基本的な概念が欠如し、数学的に無意味である。一マスの横軸が1秒、縦軸が1メートルを表す方眼はニュートン力学の説明の大前提であり、学校教育において出鱈目な方眼を無頓着に用いる教師は「グラフの傾き」についてまったく理解していないものと言える。
注意 2.
宇宙空間という「物」が存在する。そして、それとは別に、人間は頭の中では空間を幾何学的に認識することができる。点、直線、平面座標、三次元座標などは宇宙空間には実在せず、それらは人間の頭の中の数学的空間における幾何学的な認識の仕方、計算の方法である。宇宙は神秘であり、そもそも宇宙全体が移動しているかもしれないのであり、実在する物体の絶対的な移動距離は我々の知るところではない。「宇宙空間における物体の移動」と「数学的空間における物体の移動」を混同してはならない。ニュートン力学は人間の頭の中の数学的空間で語られ、それゆえに重力加速度、万有引力の法則が、物体にいかなる接触もなく、遠隔作用として力が加わる正体不明の不思議な現象として強調される。残念ながら、子供が宇宙空間と数学的空間を混同している場合のみ、慣性系という無意味な語とともに静止状態と等速直線運動が混同されたり、あるいは観察者の存在が問題となったりする。ニュートン力学は頭の中、すなわち「紙の上」の座標において語られるものであり、点 P は方眼紙の上に打たれた点 P を意味する。宇宙空間には静止状態の物体はないなどと、当たり前な、恥ずかしいことを言わないように注意すること。地球上や宇宙空間などでの話ではなく、まして「空気の抵抗はないものとする」などと断ることがそもそも出鱈目である。紙の上の座標に空気抵抗があるわけがない。
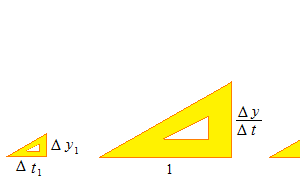
同様に、力の単位であるニュートンと質量も一目盛りが1ニュートンの縦軸と1キログラムの横軸の座標のみで意味をもつ。質量は物の重さのことであると思われがちであるが、質量と重力加速度の掛け算がニュートンであり、質量は単に存在している物体の量のみを表す。おそらく kg という単位に惑わされるのであろう。
ニュートン自身は「プリンキピア、自然哲学の数学的諸原理」では微積分による説明を避けながら記述したが、ニュートン力学は微積分の計算そのものであり、微積分を知らない子供たちは割り算を用いて感覚的に学習し、力と運動エネルギーの混同なども起こる。また、子供たちの理解力は感覚的な理解力のみであり、速度を割り算、そして加速度を引き算だと思いたがる。
1. 移動距離と経過時間
2. 速度
3. 加速度
4. 力と質量
ニュートンの力学により、我々は地球上で台秤などによる測定した物体のニュートン、すなわち秤の台を下に押す力から、その物体の質量を計算することができ、数学的ニ次元での距離の数値と経過時間の数値により、速度や加速度の数値が表されることになるのではあるが、また、逆に、むしろそれらは微積分の計算からの定義にすぎないのである。我々が知覚できる「時間(秒)」と「距離(メートル)」と「力(ニュートン)」から微積分の式によって数学的に発見される「項」の名称にすぎず、それらの「項」を直感的に、あるいは身体的な感覚として把握しようとするのは誤りである。純粋に数学的な「項」であり、言葉を用いてその「感じ」を表すこともできない。
質量とは何か。
我々が地球の表面で日常的に知っている重さは身体的感覚であり、ニュートン力学での質量とは異なる。
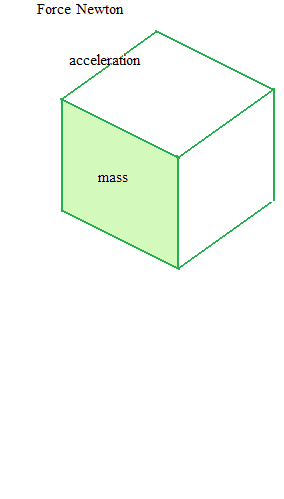
力 = 質量 × 加速度
地球の表面で、ある男性 A が体重を測定した際、体重計の中のバネが 686 ニュートンの力に対応して伸びたとする。体重計の目盛りに 686N と表示されると我々の日常生活には不向きであり、そのような体重計を購入する人は誰もいないので、質量 70Kg が表示されるように製造され販売されている。
686 = 70 × 9.8
男性 A の地球の中心に向かっての落下を体重計の抗力が阻んでいるので、686N は体重計のバネの抗力の数値であると言うべきである。男性 A と体重計は両者の位置的関係を保ったまま等速度で移動する。実際は地球の表面で力学は非常に複雑であり、一般に観測者の錯覚に満ちているので、力学の説明に用いることはできない。地球上での抗力という語も様々な力の複雑な干渉を簡略化している語にすぎない。
地球の重力加速度 9.8 m/s2
月の重力加速度 1.6 m/s2
金星の重力加速度 8.87 m/s²
木星の重力加速度 26 m/s2 (木星に関しては、いろいろな数値がある。)
男性 A が木星の表面に立つ際には、彼自身の1820ニュートンの抗力が必要である。木星の表面を歩行することは不可能。逆に、我々は地球の表面での我々自身の抗力に慣れているとも言える。
問、木星の表面で物体を落下させた場合に、最初の1秒間で落下する距離は何メートルか。
論理
ニュートン力学の理論は論理的である。論理とは、目に見えないことがらに関する正しい推論のこと。目に見えているものは、明らかであり、論理ではない。名探偵は犯人が誰かを論理的に推理する。それに対し、現行犯は論理的に犯人なのではなく、目で見て明らかに犯人である。一般的に、確率の計算方法、法律などの規則、チェスの勝敗、もしかしたら200年後に誤りと分かるような自然科学の法則の式などは、いずれも論理であり、人間の頭の中、紙の上にしか存在しない。速度、加速度、質量は計算に使われる論理的な成分であるので、我々が身体的感覚で知覚することは不可能。速度、加速度、質量は、紙の上で式の中だけで意味をもつ。視覚的に、あるいは感覚的に理解しようとするならば、そのこと自体がすでに誤解である。大切なのは、学校の数学で対数の学習が始まった時点で数学は感覚的な理解を越えるということを知るということ。加速度は微分であり、対数の計算である。視覚や身体感覚で理解するような計算ではない。視覚的と言うならば、関数のグラフの扱いのみがとても視覚的であるとも言えるのではあるが。
微分と割り算
「同じ大きさのイチゴが15個あります。三人の子供で分けるならば、一人につき何個ずつになるでしょうか」
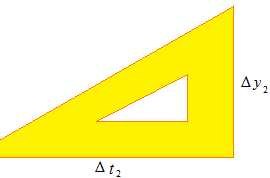
この問に、「子供は、各々、自分が5個食べるつもりのスピードで食べ始める」と答えるならば微分的と言えるかもしれない。直線グラフの場合のみ微分は単純な割り算になり、「割合」は「一単位あたりの量」に等しくなる。下の図は微分の考え方の真髄である。論理的にのみ、割り算の神秘として納得する。しばしば、1何々当たりの量などと表現されるが、微分を子供用に表現したものであり、高校生以上に用いてはならない表現である。


小さな三角マーク Δ はギリシャ文字のデルタの大文字で、アルファベットの D に対応し、この図では、t が無限小にもなりうることを表現している。
等速で直線運動をする宇宙船が1200km を 60秒間で移動した。その場合の速度は 20km/s である。速度は常に 20km/s であり、一秒ごとの移動距離が 20km であるという意味ではない。時間を横軸とし、速度の計算は移動距離の割り算ではなく、移動距離の微分である。速度は時間的な一点における速度であり、移動距離、経過時間という要素は含まれない。速度の微分が加速度である。加速度は論理的な成分であり、我々の知覚を越えているので、感覚的に理解することは不可能。加速度は速度変化のみの値であり、移動距離、経過時間、速度という要素は含まれません。
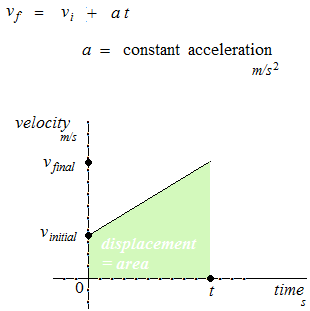
速度と加速度の単位記号 m/s , m/s2
グラフが直線である場合のみ、微分は単なる割り算と同じになる。微分の値に、簡略化のために割り算の形の単位記号 m/s や m/s2 などが付けられているが、これは曲線グラフには当てはまらない便宜上の単位記号である。
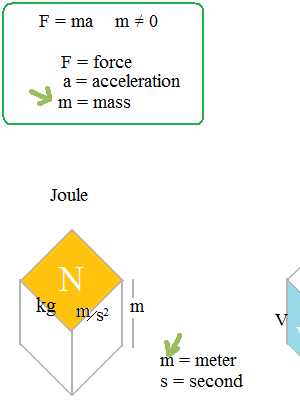
力 = 質量 · 加速度
F = ma
と書いたときは、必ず
m ≠ 0
を書く。
9.80m/s2 と 9.80N/kgの違い
加速度は、あたかも力を質量で割ったものとしての、力のように見えてしまうが、加速度は微分であり、割り算ではないので、加速度を物体の 1kg 当たりの力(ニュートン)のことである言ってしまうと誤り。加速度は力ではない。
また、子供たちが感覚的に力であると思っているものは、実は運動エネルギーである。
問の答え
木星の表面で物体を落下させた場合に、最初の1秒間で落下する距離は13m。
極端な言い方をすれば、何にせよ、微分を一回するならばそれはある種の加速度と言えるのである。
Amp ohm mho Volt Watt
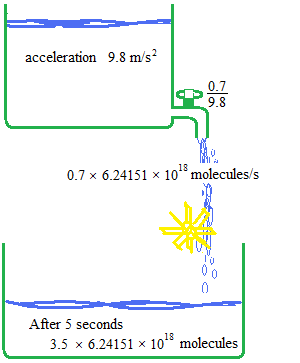
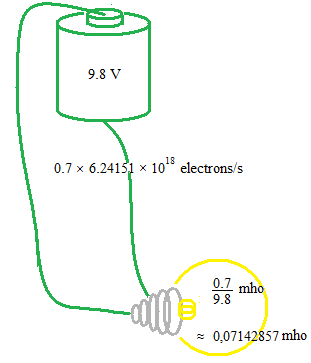
Electric current is the number of electrons flowing through the wire for a second. For example, if the electric current is constant, 0.7 amps, this means that 0.7 × 6.24151 × 1018 electrons pass through a section of the wire per second.
This is a water flow analogy to understand the electricity units.
After 5 seconds, there are 3.5 * 6.24151 * 1018 water molecules in the recipient.
The analogy between volt, acceleration and gravitation is a very Newtonian idea.
We change the number 6.24151 * 1018 into C, as Coulomb.
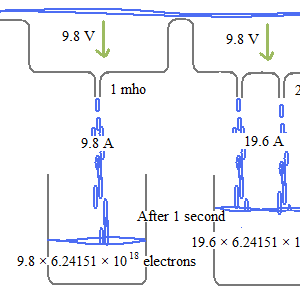
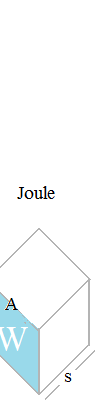
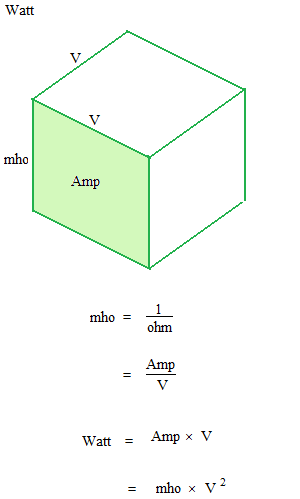
If we use ohm, the relationship between Watt and Force in Newton unit is not evident. But when we see with mho as Siemens, similarities between Ampere and mass, Volt and acceleration, are interesting.
I think the Volt is a kind of acceleration. But I never heard such a story.