Volume of regular tetrahedron
Derivative of geometric shapes
Volume of a pyramid or a cone
Volume of a pyramid or a cone is equal to 1/3 of volume of a prism or a cylinder with the same base. Why?
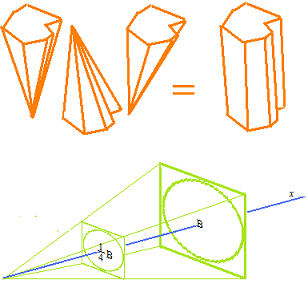
0 ≤ x Variable : height of pyramid or cone
B Constant : area of base when x = 1 .
Bx2 Area of base
f ‘ = Bx2 Limit of the Rate of change of pyramid or cone
Volume of pyramid must be…
![]()
Bx3 Volume of prism or cylinder
As the derivative of area of a circle is equal to its circumference as placing the variable x as the length of radius, so in order that the derivative of square would be equal to the sum of four sides, what value should the variable x take?
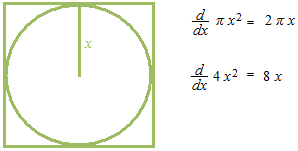
When you place x as the radius of inscribed circle, the derivative of area of square will be equal to the total of four sides.
Let’s try with a equilateral triangle taking radius of inscribed circle as x .
Is rate of change equal to the total of the length of three sides?
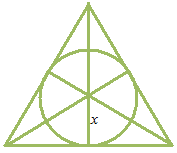
x as the radius of inscribed circle
Length of a side
![]()
Area of equilateral triangle
![]()
Derivative of volume of a sphere is equal to the value of surface area.
![]()
How about cube?
x as radius of inscribed circle
Length of a side.
2x
Volume of cube.
8×3
Surface area of cube
24×2
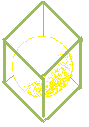
The last one, regular tetrahedron.
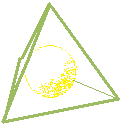
x as the radius of inscribed circle
a is the length of a side of regular tetrahedron.
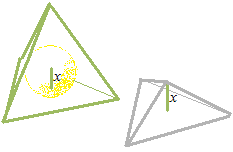
If we divide the regular tetrahedron in four triangular pyramids the base of which is one of four faces of the regular tetrahedron, the height of this small pyramid must be x.
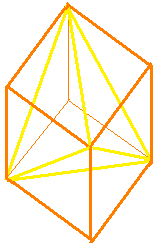
We are going to use the fact that if we tie four corners of a cube, it makes a regular tetrahedron inside.
In other words, a cube can be divided into one regular tetrahedron and four extra triangular pyramids.
Length of the side of cube.
![]()
Volume of one extra triangular pyramid.
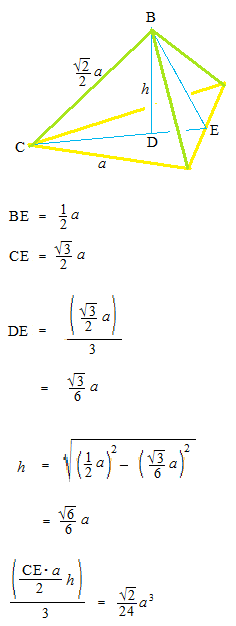
Volume of regular tetrahedron
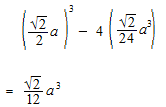
Vomume of each small triangular pyramid.
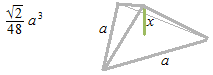
Area of the base of small triangular pyramid.
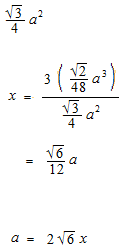
Volume of regular tetrahedron.
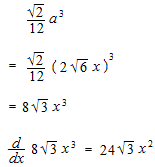
Surface area of regular tetrahedron.
![]()
x as the radius of inscribed circle.
