正四面体の体積
変化する物の関数の導関数は、その変化の大きさの関数になります。たとえば、自動車が走る場合は、距離の関数からスピードの関数になります。
立体では、体積の関数から体積の増え方の関数になります。たとえば、何々錘の体積の関数で高さを横軸にとった場合、導関数は底面積の関数になります。
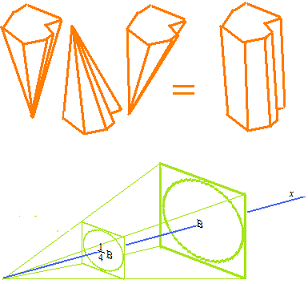
何々錘の体積は何々柱の体積の 1/3 になります。
![]()
0 ≤ x高さの変数
B定数 : x = 1のときの底面の面積
Bx2 底面の面積
f ‘ = B x2 錐の体積の変化率
錐の体積
Bx3 柱の体積
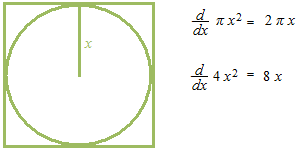
円の面積の微分は円周の値に等しいですが、正方形の面積の微分が
四辺の合計になるためには、変数をどのようにとったらよいでしょうか。
内接円の半径を x とすると四辺の合計が面積の微分と等しくなります。
内接円の半径を x にとって、正三角形で試します。
変化率は三辺の合計に等しくなるでしょうか。
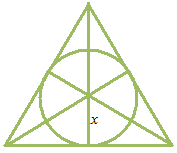
一辺の長さ
![]()
正三角形全体の面積
![]()
球の体積の微分は表面積の値に等しくなります。
![]()
では、立方体ではどうでしょうか。
![]()
立方体の内接球の半径を xにとります。
立方体の一辺の長さ
2x
立方体の体積
8 x3
立方体の表面積24 x2
最後に正四面体で試します。
正四面体の内接球の半径を xにとります。
正四面体の一辺の長さを aとします。
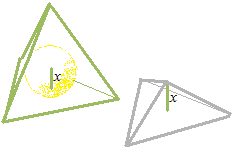
正四面体を各面を底面とした四つの三角錐に分けると、その高さが xになります。
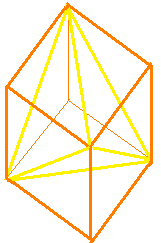
立方体の角を適当に四つ選んで直線で結ぶと、中に正四面体ができるという性質を使います。
逆の言い方をすれば、正四面体と四つの適当な三角錐を外側に組み合わせると図のような大きな立方体ができます。
立方体の一辺の長さ
![]()
まわりの三角錐ひとつの体積
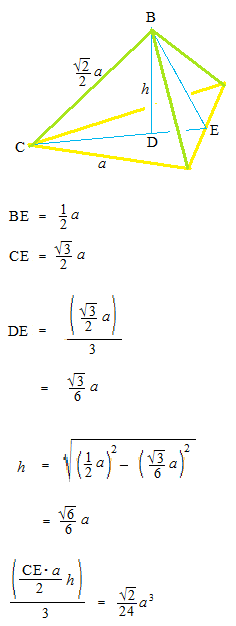
正四面体の体積
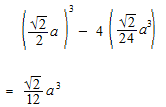
正四面体を四つに分けたときの小さな三角錐の体積。
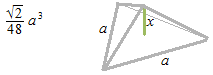
小さな三角錐の底面積。
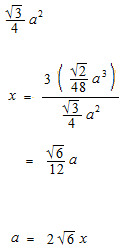
正四面体の体積。
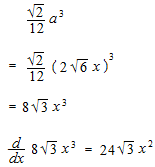
正四面体の表面積
![]()
