dx and dy are denominator and numerator of proportion, but they would be also used as small quantity of length on a graph. Namely as base and height of tiny right triangle.
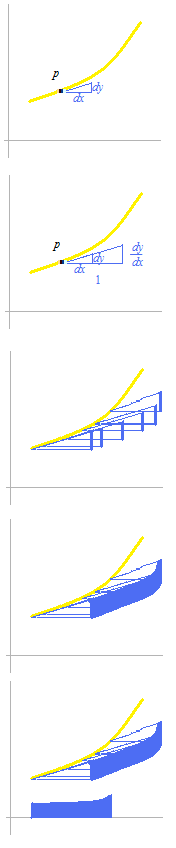
There is an upward curve in quadrant I and a point p on this curve. The slope of the tangent line of the curve at point p can be represented by the slope of the hypotenuse of a right triangle. The proportion is represented with dx and dy.
When the value of dx is 1, the height must be tangent, dy/dx .
We put a lot of similar points on the curve and tangent-height triangles with them.
When we see these dy/dx all together, it will take a form of a bande.
And we slide this bande horizontally 1 to the left side and slide down until the every part of the base border of the bande touches the x-axis, the upper border of the bande becomes derivative curve.
Now, if we consider dx as very small length, putting small triangles in chain from the left to the right, the sum of all dy will be the value of the difference of y. We get the initial graph, the antiderivative. Namely, the sum of (dy/dx)×dx will be the value of y.
But if the position of the starting point of the summation is not determinated, the height of the whole curve will not be determinated.
