dx と dy は微分に於ける比率の分母と分子なのですが、定積分の理解のためにはこれらをとても細かい長さとする考え方も否めません。極小直角三角形の底辺と高さとする考えです。
第一象限に右上がりの曲線 f(x)があります。その曲線上の点 p 付近の曲線の傾きを、直角三角形の斜辺の傾きで表します。その直角三角形の底辺と高さの割合を dx と dy で表します。 この直角三角形の底辺を 1 とすると高さは dy/dx になります。
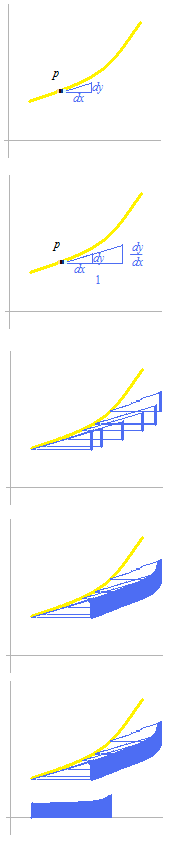
曲線上にさらに沢山の点を置いていきます。そのつど底辺 1 の直角三角形を作っていきます。それらの直角三角形のそれぞれの高さの辺を全部まとめて見ると、帯のような形になります。
この帯を左に1だけ平行移動して、帯の下の縁が x 軸に着くまで下ろすと導関数のグラフになります。
逆に、三角形の底辺の長さを dx としたとき、左下の方から三角形を数珠繋ぎにすると、 dyの合計が yの値になる。つまり、(dy/dx)×dxを合計すると最初の曲線の形が求められます。しかし曲線全体の上下の位置は定まりません。
