平均変化率の極限、タンジェント
変化ということを問題にするときは、やはり時間をグラフの横軸にとることが多くなります。いつからいつまでにどのくらい変化するかという問題になります。自動車が2時間かけて160 km走ると平均時速は
80 km/h。
Usain Boltが9.58秒かけて100m走ると平均時速は
37.78…km/h。
どちらも距離 / 時間で計算します。
Usain Boltは0.00266…時間かけて0.1km走った。
平均時速は37.78…km/h。
測定開始時の時刻 a での位置と測定終了時の位置から計算されるので答は平均値になります。
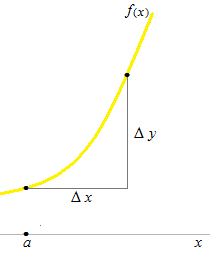
測定開始時の時刻 a から測定終了時の時刻までの時間を Δx とします。
測定開始時の位置 f (a)から測定終了時の位置までの距離を Δy とします。
平均とは、言い換えれば、測定開始時と測定終了時が離れていて、2点間に間隔があるということです。2点のそれぞれの数値のみ、つまり両端での数値のみで計算が行われ、その間での数値は無視されます。それが平均ということです。
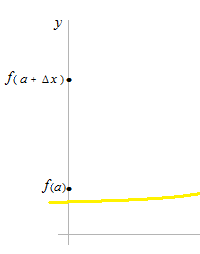
平均を A km/h とすると次のような式になります。
![]()
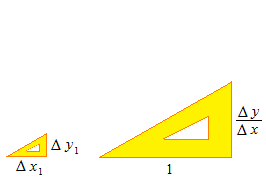
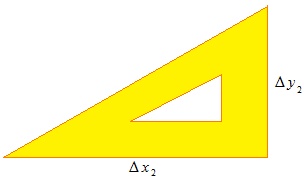
微分積分では三角関数の変数として角度ではなく単位円の弧の長さを用います。
直線の傾きを表すのには角度ではなく、縦と横の比率をもちいます。この比率がタンジェントです。
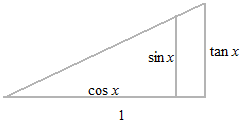
タンジェントはふたつの数値の比率を長さで表します。
タンジェントは Δx に於ける Δy の平均です。平均変化率はタンジェントで表されます。
面積は高さ 1 の体積です。
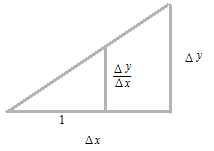
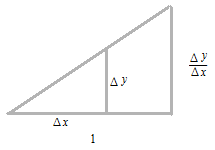
Δx にを限りなく 0 に近づけたときの、極限として一点に於ける曲線の接線の傾きの値を微分係数といいます。或る関数の微分係数を出す関数を導関数といいます。
この割り算の分子と分母をそれぞれ dy 、 dx と書きます。
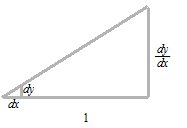
dy と dx は比率の分子と分母なので単独では用いられません。
Δx は長さ、 dx は比率の分母なのですが、微分をするときは、 Δx を dx のように扱い、
積分をするときは、 dx を Δx のように扱います。
