極限
ディジタルの極限はアナログに収束しますが、ただ細かくするということだけならば、一点に収束する必要はありません。また、定関数、一次関数ならば傾きは細かくする必要もなければ、まして一点に於ける傾きとする必要もないはずです。
数学では次のようなグラフを[a , b] では連続していないといいます。
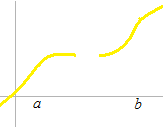
或る点で連続しているというのは、その点を極限値として関数が収束するということです。どこをとってもその点に向かう数列に属していることを連続しているといいます。本当に数と数がつながっているという意味ではありません。或る関数が [a , b] で連続。端まで続いています。
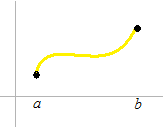
p では微分可能ではありません。点の左右で傾きがちがいます。
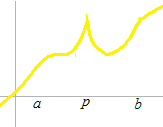
或る関数が( a , b)で微分可能。端の変化は定義できません。
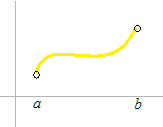
特別な場合をのぞいて、( a , b) で微分可能、[ a , b]で連続という記述はしばしば省略されますが、学校のテストなどでは必ず定義域を書いてください。特に、分数の分母に 0 がこないようにします。
極限
微分で曲線の接線の傾きを求めるとき、つまり或る関数の導関数を求めるとき、なぜ極限の考えが必要なのでしょうか。定関数や一次関数を微分する場合でもなぜ極限が必要なのでしょうか。
定関数や一次関数を微分する場合でも極限が必要である理由。
極限を求める式で答が数値で出るときを、その値に収束するといいます。その値に確かに追い詰められていく状態です。簡単な式の場合は明らかに答が出ますが、いつもとは限りません。極限は微積分の理論的な要でもあるだけに、直感的な答え方だけでは不十分です。
極限値の普通の求め方、さらにロピタルの定理による求め方があります。ロピタルの定理はあとのほうで直感的な理解とともに説明してあります。極限を求めていくとき、分子分母がともに無限であったり、ともにゼロであるような分数の型のときには分子分母をそれぞれ微分するというものです。とても便利な方法です。
極限は微分で曲線の接線の傾きを求めるとき、そして定積分で曲線の下の面積を求めるときに使われます。
導関数は関数ですから、ひとつの xに対してひとつの yが出ます。
f'(x1) = y1
変化率はふたつの xの間 に於ける yの変化です。
![]()
x1と x2の間の Δ xを絞って、ただひとつの xの値とします。
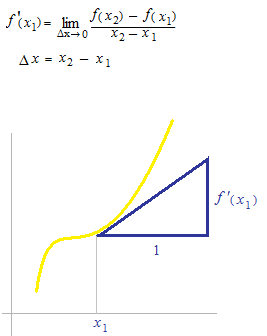
微分のことをよく曲線の接線の傾きといういい方をしますが、そもそもは接線ではありません。ふたつのxの間の平均変化率です。
平均の極限の値にしないと導関数の変数としての xの値になりません。
導関数は関数ですから、ひとつのxに対してひとつの y が出ます。
定関数や一次関数を微分する場合でも極限は必要です。
いったん導関数になったら、もう二点の差ではなく、接線の傾きというしかありません。
なぜ極限にするかというと、それは平均の極限値が導関数の横軸の変数になるからです。
無限に狭めていっても最後まで二点間にのこっているのが先の方で説明するラグランジュの平均値の定理の点です。二点間に於ける 平均値が、一点に於ける値となり、導関数の横軸の変数と導関数の値になります。この平均値の定理の点が微分の柱になります。
