Applications réciproques et leurs dérivées
En anglais, les applications réciproques s’appellent inverse functions, lorsque, en français, la fonction inverse désigne y = 1/x
Si la fonction identité y = x est considérée comme une fonction composée de deux fonctions, infiniment de paires de applications réciproques sont possibles.
Fonction composée Applications réciproques

Imaginez justement une machine qui multiplie par trois la monnaie que vous avez mise. Quand vous mettez une pièce, trois pièces sortiront. Également, une autre machine qui en fera un tiers quand vous mettez des pièces.
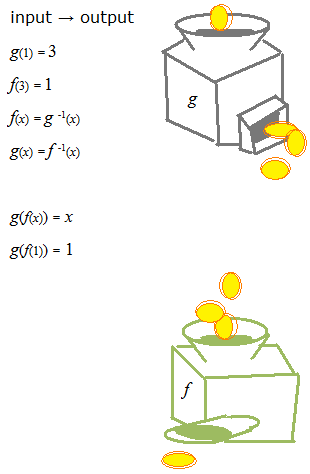
Si l’on met ces deux machines ensemble, une pièce sera toujours une pièce.
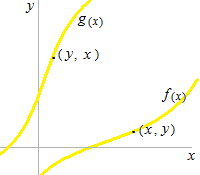
Quand il y a un point (x, y) sur f(x) , il y a toujours un point (y, x) sur g(x). Il en résulte que les graphiques de f(x) et g(x) sont symétriques l’un de l’autre par raport à la fonction identité y = x
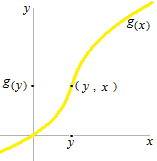
Quand on parle des applications réciproques, on mélange souvent le nom d’axe et la valeur éventuelle de variable.
Point (y , x) veut dire que un point (x, y) a une valeur y pour x, et une valeur x pour y. Ici, g (y) veut dire qu’il y a une fonction g (x) et la variable x prend eventuellement la valeur y.
Il peut arriver que la variable indépendante est de l’axe vertical dans une intégration. Mais, quand ce sont les fonctions réciproques qui sont au sujet, la variable est de l’axe horizontal.
Cela serait plus clair si le point était exprimé (a, b) ou (y1 ,x1) ou encore (u1 ,x1), mais comme il s’agit des fonctions, ce n’est pas un nombre mais une variable qui se trouve entre parenthèses.
y qui est entre parenthèses de g (y) est la réponse, l’image, de f(x) . “Quand f(x) est d’ y ” et “Quand x de g(x) est d’ y ” se passent simultanément.
x de g (x) est le nom de variable, nom de l’axe horizontal.
y de g(y) est la valeur éventuelle de variable x .
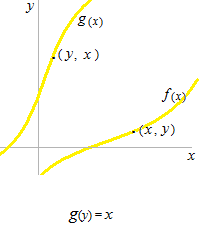
Pour que deux fonctions soient réciproques, chaque fonction doit être bijective.
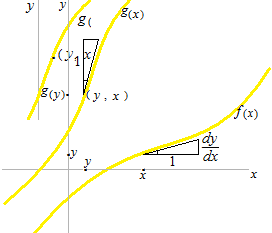
Comme les courbes de deux fonctions réciproques sont symétriques par rapport à la droite de y = x , les triangles de leurs dérivées sont aussi symétriques les uns des autres. La dérivée d’une fonction composée qui est constituée d’une paire d’applications réciproques est de 1.
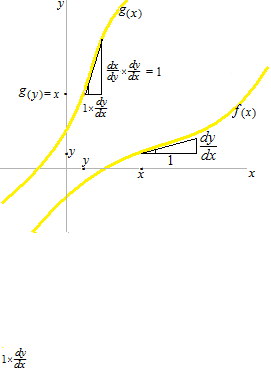
Cela veut dire qu’en ce qui concerne 1 comme ∞ fois dy, il est de la différente mesure que 1 comme ∞ fois dx .
Il y aurait deux systèmes de coordonnées.
Cependant comme ∞ est pas un nombre, l’expression ” ∞ fois dy ” n’est pas authentique.
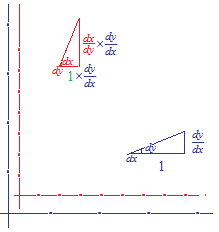
La règle de la chaine sera employée.
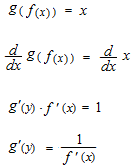
Ce n’est pas la même chose que l’équation des droites perpendiculaires.
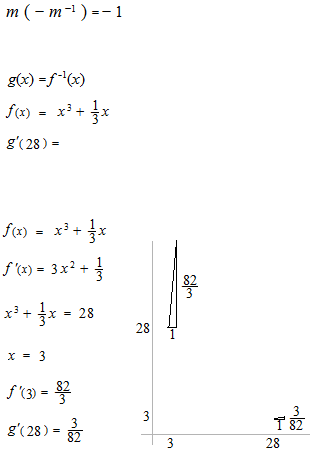
Ça peut être un calcul mental.
