Einheitskreis


“Gestern habe ich ein Lied komponiert.”
“Wie ist die Melodie?”
“Zum Beispiel ist die fünfte Achtel des dritten Taktes ein Es.”
Die trigonometrischen Funktionen und der Einheitskreis.
Die Kurve der Sinusfunktion ist eine schöne Kurve, die die Steigung von 45 Grad, die Länge der π und den Flächeninhalt von 2 hat. Die Bewunderung der Schönheit dieser Kurve könnte die Grundlage für das Verständnis der trigonometrischen Funktionen sein. Auf der einen Seite, ist die Form der Kurve der Sinusfunktion für die Differential-und Integralrechnung sehr nützlich, auf der anderen Seite, ist der Einheitskreis nur eine Abbildung, die die Definition der Sinusfunktion visuell zeigt, und anderweitig nutzlos.
Der Einheitskreis ist nicht die Sinusfunktion. Der Einheitskreis macht Illusionen, daß der Einheitskreis die trigonometrischen Funktionen zeigt, daß die Sinusfunktion und die Kosinusfunktion die Kreisbewegung des Punktes-P auf dem Kreis zeigt, und daß der Sinusfunktion und der Kosinusfunktion in der zweiten, der dritte und der vierte Quadrant geometrische betrachtet werden. Nachdem die Kurve der Sinusfunktion gemacht worden ist, braucht die Berechnung nicht mehr den Einheitskreis.
Während es sechs trigonometrische Funktionen sind, sind die Kosekansfunktion, die Sekansfunktion und die Kotangensfunktion Vereinfachungen der Sinusfunktion und der Kosinusfunktion, die in der Form der Fraktion sind. Es sind Vereinfachungen für das Schreiben von Berechnungen und für die Auswendiglernen von vielen trigonometrischen Formeln. Die Kosekansfunktion, die Sekansfunktion und die Kotangensfunktion haben keine spezifische Bedeutung. Während die folgenden Abbildungen diese Funktionen mit Längen von Strecken zeigen können, wäre es ein Fehler, die Bedeutungen der Kosekansfunktion, der Sekansfunktion und der Kotangensfunktion auf dem Einheitskreise zu betrachten. In den folgenden Abbildungen haben nur Sinus und Kosinus visuellen Bedeutungen.
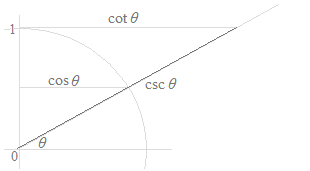
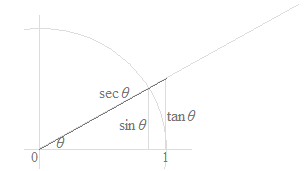
Als Kurven, werden nur die Kurven der Sinusfunktion und der Kosinusfunktion verwendet, und die Kurven der Tangensfunktion, der Kotangensfunktion, der Sekansfunktion und Kosekansfunktion sind nutzlos.
Tangente
Tangente ist die Steigung m einer Kurve im kartesischen System, und es ist nicht der Winkel θ des Einheitskreises. Tangente und der Einheitskreis haben keine direkte Beziehung.
P( cosθ , sinθ )
Der Punkt P scheint wie ein Punkt, aber in Wirklichkeit ist es ein Kreis. Der Punkt P ist der Einheitskreis, und es ist keine Funktion.
Während der Punkt P eine kreisförmige Bewegung mit einer konstanten Geschwindigkeit ist, ist der Sinus eine vertikalen Auf-und Abbewegung mit einer ändernden Beschleunigung.
Die wechselseitige Beziehung zwischen der Kurve der Sinusfunktion und der Kurve der Kosinusfunktion wird in der Berechnung verwendet werden.
y = sin x
y = cos x
