Circunferencia trigonométrica


“Ayer me compuso una canción.”
“¿Cómo es la melodía?”
“Por ejemplo, la quinta corchea de la tercera compás es un mi bemol.”
Las funciones trigonométricas y la circunferencia trigonométrica.
La curva de la función seno es una hermosa curva, que tiene la pendiente de 45 grados, la longitud de π y el área de 2. La admiración por la belleza de esta curva podría ser la base de la comprensión de las funciones trigonométricas. Por un lado, la forma de la curva de la función seno es muy útil para el cálculo diferencial e integral, por otro lado, la circunferencia trigonométrica es sólo una figura que muestra visualmente la definición de la función seno, y esta figura es de otro modo inútil.
La circunferencia trigonométrica no es la función seno. La circunferencia trigonométrica da ilusiones que la circunferencia trigonométrica muestra las funciones trigonométricas, que la función seno y la función coseno son el movimiento circular del punto P en el círculo, y que la función seno y la función coseno se consideran geométricamente en el segundo, el tercero y el cuarto cuadrante. Una vez se ha hecho la curva de la función seno, el cálculo no necesita más la circunferencia trigonométrica.
Mientras que hay seis funciones trigonométricas, la cotangente, la secante y la cosecante son simplificaciones del seno o del coseno, que son en la forma de fracción. Estas son simplificaciones para la escritura de cálculos y para la memorización de muchas fórmulas trigonométricas. La cotangente, la secante y la cosecante no tienen ningún significado específico. Mientras que las figuras siguientes pueden representar estas funciones con las longitudes de segmentos de línea, sería un error considerar los significados de la cotangente, de la secante y de la cosecante en la circunferencia trigonométrica. En las figuras siguientes, sólo el seno y el coseno tienen significados visuales.
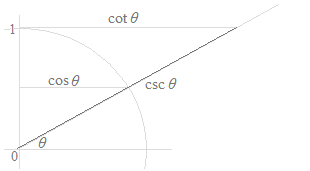
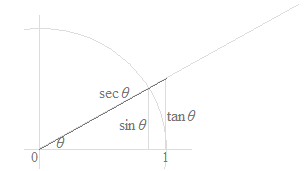
Como curvas, sólo las curvas de la función seno y la función coseno se utilizan, y las curvas de la función tangente, la función cotangente, la función secante y la función cosecante son inútiles.
Tangente
La tangente es la pendiente m de una curva en el sistema cartesiano, y no es el ángulo θ de la circunferencia trigonométrica. La tangente y la circunferencia trigonométrica no tienen relación directa.
P( cosθ , sinθ )
El punto P parece como un punto, pero, de hecho, es un círculo. El punto P es la circunferencia trigonométrica, y no es una función.
Mientras que el punto P es un movimiento circular a una velocidad constante, el seno es el valor de un movimiento ascendente y descendente con una aceleración que cambia.
La relación recíproca entre la curva de la función seno y la curva de la función coseno se utilizará en el cálculo.
y = sin x
y = cos x
