Unit circle


“Yesterday, I wrote a song.”
“What’s the melody like?”
“For example, the fifth eighth note of the third bar is E flat.”
The trigonometric functions and the unit circle.
The curve of the sine function is a beautiful curve which has the slope of 45 degrees, the length of π and the area of 2. The admiration for the beauty of this curve could be the basis of the understanding of the trigonometric functions. On the one hand, the shape of the curve of the sine function is very useful for the differential and integral calculus, on the other hand, the unit circle is just only a figure which visually shows the definition of the sine function, and it is otherwise useless.
The unit circle is not the sine function. The unit circle gives illusions that the unit circle is showing the trigonometric functions, that the sine function and the cosine function are the circular motion of point P on the circle, and that the sine function and the cosine function are considered geometrically in the second, the third and the fourth quadrant. Once the curve of the sine function has been made, the calculation does not need any longer the unit circle.
While there are six trigonometric functions, cotangent, secant and cosecant are simplifications of sine or cosine, that are in the form of fraction. These are simplifications for the writing of calculations and for the memorization of many trig formulas. Cotangent, secant and cosecant have no specific meaning. While the figures below can represent these functions with the lengths of line segments, it would be a mistake to consider the meaning of cotangent, secant and cosecant on the unit circle. In the figures below, only sine and cosine have visual meanings.
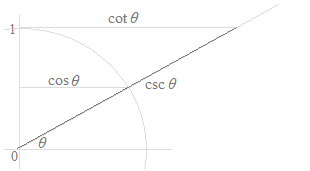
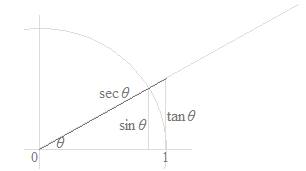
As curves, only the curves of the sine function and the cosine function are used, and the curves of the tangent function, the cotangent function, the secant function and the cosecant function are useless.
Tangent
Tangent is the slope m of a curve in the Cartesian system, and it is not the angle θ of the unit circle. Tangent and the unit circle and have no direct relation.
P( cosθ , sinθ )
The point P looks like a point, but in fact, it is a circle. The point P is the unit circle, and it is not a function.
While the point P is a circular motion at a constant speed, sine is the value of an up and down movement with a changing acceleration.
The reciprocal relationship between the curve of the sine function and the curve of the cosine function will be used in the calculation.
y = sin x
y = cos x
