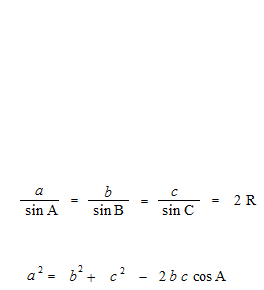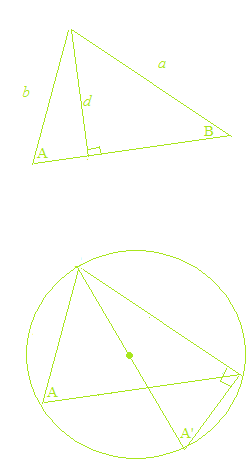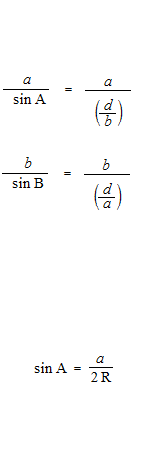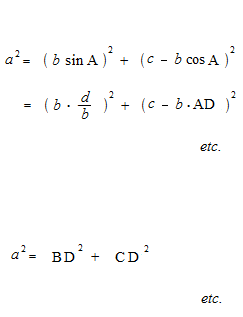Rapports trigonométriques d’un angle obtus, loi des sinus, loi des cosinus
Le sinus d’un angle obtus, le cosinus d’un angle obtus
Les rapports trigonométriques
Le sinus, le cosinus et la tangente sont des ratios entre les longueurs des côtés d’un triangle rectangle. Ce sont des rapports entre les longueurs de deux côtés, qui sont des valeurs absolues. Le sinus, le cosinus et la tangente ont été définis seul pour les côtés d’un triangle rectangle. ¤Il n’y a pas de sinus d’un angle obtus, cosinus d’un angle obtus, tangente d’un angle obtus.
La loi des sinus avec un angle obtus et la loi des cosinus avec un angle obtus
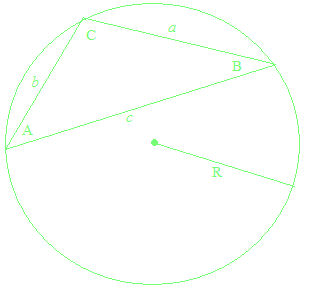
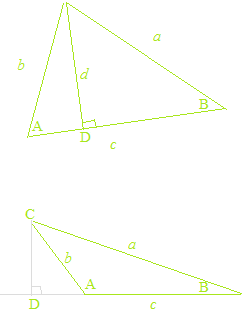
En prenant, pour le sinus d’un angle obtus, la valeur du sinus de son angle supplémentaire, et pour le cosinus d’un angle obtus, la valeur du cosinus de son angle supplémentaire, la loi des sinus et la loi des cosinus sont valables même pour les triangles obtus.
La loi des sinus et la loi des cosinus sont de la géométrie pure, et cela n’a rien à voir avec les fonctions trigonométriques. Également, dans les démonstrations de la loi des sinus et de la loi des cosinus, on utilise la valeur du sinus de l’angle supplémentaire pour le sinus d’un angle obtus, et la valeur du cosinus de l’angle supplémentaire pour le cosinus d’un angle obtus. Comme la géométrie, le calcul est toujours avec des valeurs absolues. Par la confusion des fonctions trigonométriques et les rapports trigonométriques, des explications de la loi des sinus et de la loi des cosinus avec les fonctions trigonométriques et le cercle trigonométrique sont évidemment des erreurs. Parfois, il y a des explications erronées, telles que “le sinus d’un angle obtus et le sinus de l’angle aigu ont la même valeur”, etc.
Fonction
En général, les fonctions sont des opérations avec une variable indépendante, qui déterminent une seule valeur de la variable dépendante, et les fonctions peuvent être librement créées avec des définitions librement choisies. Par exemple, une fonction peut être créée avec une variable indépendante pour les dates et une variable dépendante pour la température à midi à New Delhi.
Le sinus d’un angle obtus et le cosinus d’un angle obtus
Les rapports trigonométriques ne peuvent pas être utilisés pour un angle obtus. Il était une fois, un mathématicien qui a inventé deux fonctions. Ces fonctions ont été définies comme les rapports trigonométriques dans le premier quadrant du cercle trigonométrique, puis, avec la symétrie verticale et horizontale. Elles représentaient des valeurs positives ou négative de longueur, et ce n’étaient pas des ratios des valeurs absolues. Le cercle trigonométrique était une manière de montrer les définitions. Le mathématicien a nommé ces deux fonctions, qui ont été artificiellement définies, “la fonction sinus” et “la fonction cosinus”. Les rapports trigonométriques ne peuvent jamais être utilisés pour les angles obtus. Ce monsieur a fabriqué deux fonctions qui ont la rotation comme définition, et les a nommé “la fonction sinus” et “la fonction cosinus”.
La loi des sinus et la loi des cosinus