Warum die Argumente der trigonometrischen Funktionen sind im Bogenmaß.
π ist eine irrationale Zahl, 3,14159265359…
„Mit Radiant rechnen“ bedeutet, den Punkt 3,14159265359… auf der horizontalen Achse eines Koordinatensystems mit π zu bezeichnen und alle anderen Werte auf dieser Achse in Abhängigkeit von π auszudrücken.
„Mit Radiant rechnen“ bedeutet, „π auf der horizontalen Achse eines Koordinatensystems zu verwenden“.
Ein Winkel, eine zweidimensionale geometrische Größe, die unabhängig von der Größe der gezeichneten Figur ist, wird als eindimensionale Größe ausgedrückt: „das Verhältnis des Bogens zum Radius“, also „die Länge des Bogens, wenn der Radius gleich 1 ist“.
Das Argument ist der Wert für die unabhängige Variable einer Funktion. Es ist der Wert, der in die Variable x einer Funktion f(x) gesetzt wird.
Ohne Differential-und Integralrechnung, wären die trigonometrische Funktionen nicht in Gebrauch. Während es oft Graphen von den trigonometrischen Funktionen unter Verwendung Koordinaten gibt, wo die Breite der Skale der horizontalen Achse und die Breite der Skale der vertikalen Achse unterschiedlich sind, ist es notwendig, diese Skalen der Achsen zu vermeiden, weil Steigung und Fläche bei der Differential-und Integralrechnung unerlässlich sind.
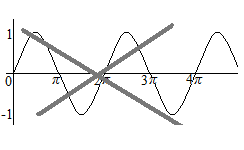

Die Koordinaten für Graphen der Differential-und Integralrechnung müssen die gleiche Breite der Skala für die horizontale Achse und die vertikale Achse haben. Es existiert nur eine “Form” der Kurve der Sinusfunktion; die Höhe ist zwischen 1 und −1, und der Zykluslänge ist 6.28…, mit einziger Skala. Kurven, die horizontal Kurzform haben, hat nicht die Form der Kurve der Sinusfunktion, auch wenn ihre Schnittpunkte mit π markiert worden sind. Dies ist eine sehr grundlegende Idee der Differential-und Integralrechnung.
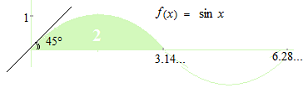
Die Verwendung von Radiant für die trigonometrische Funktionen bedeutet, daß die Periode der Kurve der Sinusfunktion 6,28… ist, mit 1 auf der vertikalen Achse. Als die grafische Darstellung von Elektrizität durch einen elektrischen Generator mit der Drehung eines Stromleiters in magnetischen Feldlinien, die vertikale Achse ist die Spannung und die horizontale Achse ist die zweite, daher ist die Kurve von 1 Volt mit Frequenz 0,159… Hz die einzige Kurve der Sinusfunktion in der Differential-und Integralrechnung.
Die Flächeninhalt unter 1/2 Kurve der Sinusfunktion ist 2 .
Wenn x = 0, die Steigung der Kurve der Sinusfunktion ist 45 Grad, d.h., 1.
Die Steigung der Kurve der Sinusfunktion auf x1 ist gleich der Wert von cos x1
Die Beziehung zwischen y = − cos x + c und y = sin x
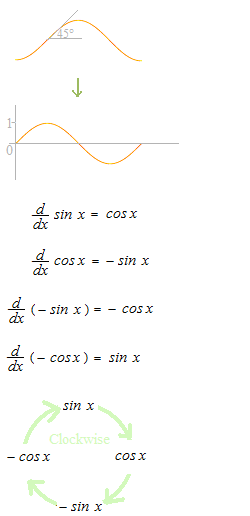

Als eine klare Beschreibung der Definition der Sinusfunktion, auf dem Einheitskreis, mit der Winkel θ als die unabhängige Variable, kann der abhängige Variable von dem Werte, der nach oben und unten bewegt, auf der vertikalen Achse vorgestellt werden.
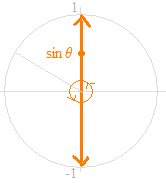
Die Position in der Bewegung; sin θ
Die Geschwindigkeit der Bewegung; cos θ
Die Beschleunigung der Bewegung; − sin θ
Die Kurve der Sinusfunktion mit der Periode 6,28 … ist ein wichtiges Werkzeug für die Differentialrechnung.
