Perché gli argomenti delle funzioni trigonometriche sono in radianti.
L’argomento è il valore per la variabile indipendente di una funzione. In generale, è il valore che sarà messo nella variabile x di una funzione f(x) .
Senza calcolo differenziale e integrale, le funzioni trigonometriche non sarebbero in uso. Mentre ci sono spesso grafici delle funzioni trigonometriche utilizzando coordinate in cui la larghezza della scala dell’asse orizzontale e la larghezza della scala dell’asse verticale sono differenti, è necessario evitare queste scale degli assi, come la pendenza e l’area sono essenziali nel calcolo differenziale e integrale.
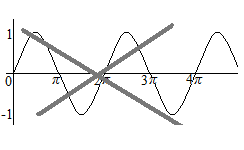
Le coordinate per grafici del calcolo differenziale e integrale devono avere la stessa larghezza della scala per l’asse orizzontale e l’asse verticale. C’è solamente una “forma” della curva della funzione seno; l’altezza è tra 1 e −1, e la durata del ciclo è di 6,28…, rispettando scale uguali. Curve che sono orizzontalmente corte non hanno la forma della curva della funzione seno, anche se le loro intersezioni sono marcate con π. È una idea elementare del calcolo differenziale e integrale.
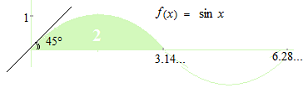
L’uso di radianti per le funzioni trigonometriche significa che il periodo della curva della funzione seno è di 6,28… rispetto a 1 sull’asse verticale. Come una rappresentazione grafica dell’energia elettrica da un generatore elettrico con la rotazione di un conduttore in linee del campo magnetico, l’asse verticale è la tensione e l’asse orizzontale è il secondo, pertanto, la sinusoide di 1 volt, frequenza di 0,159… Hz è la sola curva della funzione seno nel calcolo.
L’area sotto 1/2 curva della funzione seno è di 2.
Quando x = 0, la pendenza della curva della funzione seno è di 45 gradi, cioè, 1. La pendenza della curva della funzione seno a x1 è uguale al valore di cos x1
La relazione tra y = − cos x+ c e y = sin x
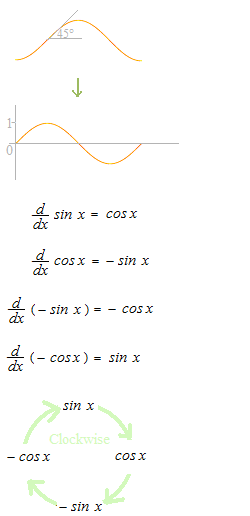
Come una chiara descrizione della definizione della funzione seno, sul cerchio unitario, con l’angolo θ come variabile indipendente, la variabile dipendente può essere rappresentata dal valore che si muove verso l’alto e verso il basso sull’asse verticale.
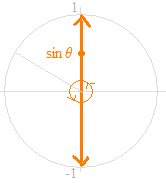
La posizione nel movimento; sin θ
La velocità del movimento; cos θ
L’Accelerazione del movimento; − sin θ
La curva della funzione seno con il periodo di 6,28 … è uno degli strumenti fondamentali del calcolo differenziale.