なぜラジアンを使うのか
π は 3.14159265359… という無理数である。
「計算にラジアンを使う」とはグラフの横軸上の 3.14159265359… という点を π と置いて、その他の横軸上の数値をすべて π を使って記するということである。
「計算にラジアンを使う」とは、「グラフの横軸に π を使う」ということ。
図形的、二次元的な数値「角度」、描かれた図形そのものの大きさとは無関係な形としての「角度」を、「半径に対する円弧の割合」、すなわち「半径を1とした場合での円弧の長さ」という一次元的な数値で記すこと。
なぜラジアンを三角関数の引数に使うのか。
関数の独立変数が取る数値を引数 (ひきすう、argument) と呼ぶ。
引数は関数 f(x) の変数 x の取る数値である。
微積分の計算なくしては三角関数に意味はない。しばしば縦軸の目盛りの幅と横軸の目盛りの幅が違う座標を使った三角関数のグラフを目にするが、微積分は曲線の傾きや曲線によって囲まれた部分の面積の計算であるから、そのような座標軸の目盛りはグラフとして出鱈目である。
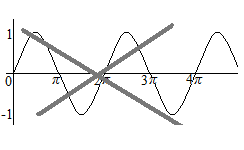

微積分のグラフの座標は縦軸の目盛りと横軸の目盛りが同じ幅でなくては意味がない。サイン関数の曲線の形は、ひとつだけ。上下がプラス1とマイナス1、周期が 6.28…を方眼の目盛りを尊重して描いたもの。横幅が詰まったグラフは、たとえ交点に π と記してあったとしても、「形」がサイン関数の曲線ではない。これは微積分の素朴な基本。
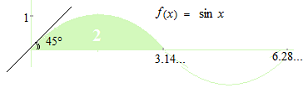
「三角関数にラジアンを使う」とは、サイン関数の曲線の周期が縦軸の1 に対して 6.28… であることを意味する。磁力線の中での導体の回転を使った交流発電のグラフ、縦軸がボルト、横軸が秒であるから、電圧1ボルト、周波数 0.159…ヘルツの曲線が微積分における唯一のサイン関数の曲線の形。
1/2のサイン関数の曲線の下の面積は 2。
x = 0のところでのグラフの傾きは 45 度、すなわち 1 。
サイン関数の曲線の x1 における接線の傾きは cosx1 の値に等しい。
y = − cosx+ c と y = sinx との関係
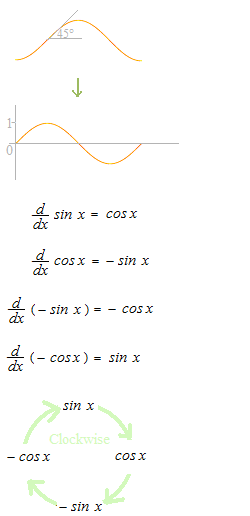

サイン関数の定義の明瞭な記述として、単位円を使い、独立変数を角度 θ、従属変数を縦軸上を上下運動する値で表すことができる。
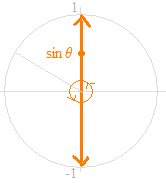
上下運動の位置; sin θ
上下運動の速度; cosθ
上下運動の加速度; −sinθ
周期が 6.28…のサイン関数の曲線の形は、微積分の主要な道具。
