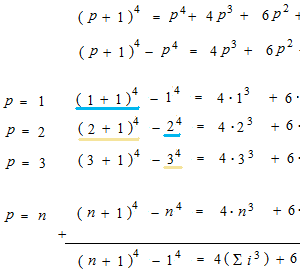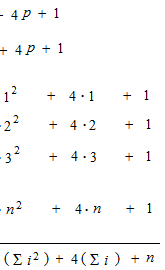Sigma notation for definite integral
Sigma notation makes an expression with n as using an expression with i. Sigma erases i in operation of summation.
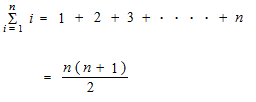
Summation starts always at i = 1. Don’t start at i = 0 except for a very very special case.
Summation ends at n. Never put a number instead of n, or sigma will not make any sens.
For i will be erased, there is no need for the second, the third term, etc. Sigma notation must be written like this.
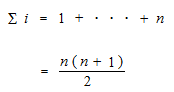
We, human being, have this pattern of expression n ( n + 1 ) / 2 from the beginning of history.
This expression is now called sigma i. Sigma i is written with n. i is erased.
![]()
Cavemen must have found also this one that we call sigma i2
![]()
Changing general term with i into sum with n. When n is infinitely big, 1/ n will be erased too.
Then the result is definite integral.
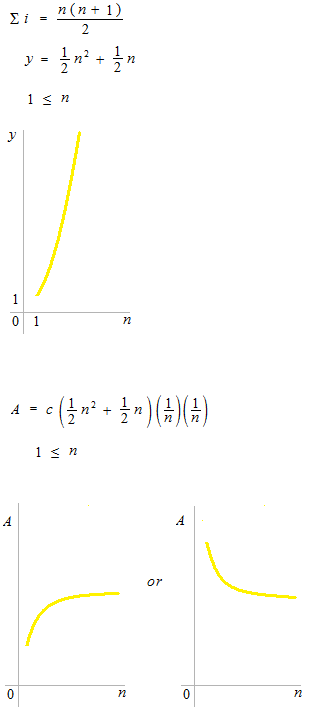
Intuitionaly sigma is a sort of triangle. If we make a multiplication between sigma and some quantity, we will obtain the sum of all. For a function of m power, curve of sigma im is increasing, because it has nm+1. Multiplying by height (1/n)m , and by width (1/n) , area function converges to a number value. Simplicity of sigma in the addition in the general term promises the possibility of area calculation.
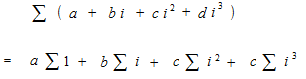
Sigma summation is an addition. This addition is the fundamental thing of the integration.
Arrange balls in square and then dIvide into two parts.
1 + 2 + 3 + 4 + ∙ ∙ ∙ ∙ + n
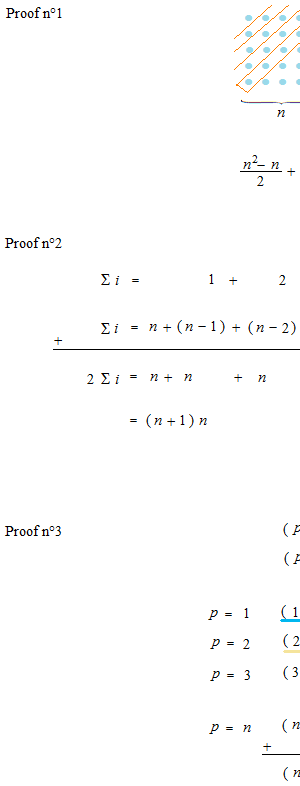
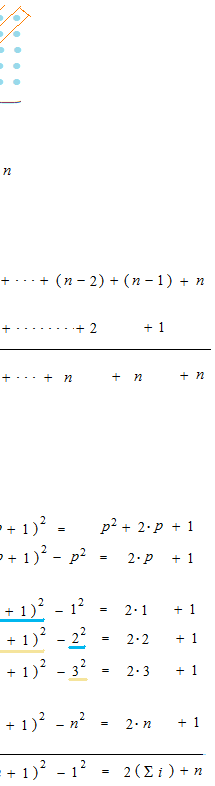
This method can be used for i in heigher power.
![]()
It is not necessary to counte always by means of a diagram, but volume of pyramid makes counting possible. Let’s consider that a solid is a cluster of balls. In order to count balls of pyramid, before we divide the triangular prism by three, we must take the joint face and divide and add it. Now, we are going to count the number of this pyramid, which we divide into two parts.

If we try to count, it must be in four dimensions.
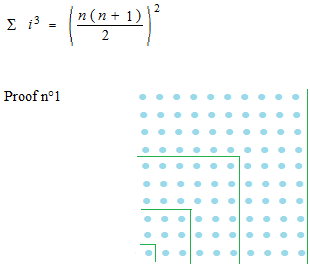
In the plane, it can be like this.
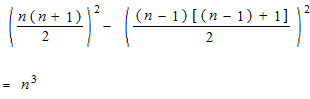
We can use a mean trick like this.