シグマ記号
シグマ記号はi を使った式をn を使った式に変えることを目的とします。n 個に分割したものの i 番目という式から、それを合計して i を消すという働きをします。
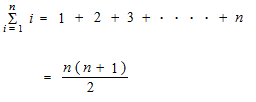
シグマ記号での総和は必ず 1 から始まります。特殊な場合を除いて、0 から始めたりしないで下さい。シグマ記号の総和の上限は n しか来ません。定数が来たらシグマ記号を使う意味がありません。そして結果として、何番目ということが消されるわけですから、2番目、3番目の項も書く必要はありません。
本当のシグマ記号の書き方は数学では下のようになります。
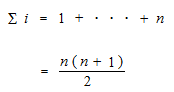
さらに、考え方の順序としてまず何千年も前からこの型 n(n+1)/2があったのです。この型を現代人はシグマiと呼びます。
シグマi はn を使って書かれます。
i は既に消されています。
![]()
原始人も見つけていた下の型をシグマi2と呼びます。
![]()
何番目がどうようになっているかという i を使った式が、全部でどのくらいかという n を使った式に変わり、1/ n の n を無限にすると n も消えて、定数の答が出るのが定積分です。
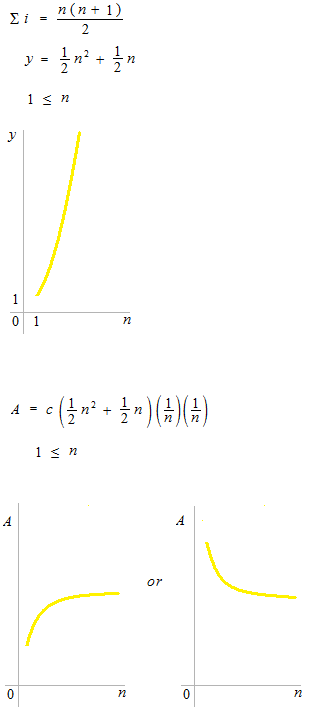
直感的にはシグマは三角形かピラミッドのようなもので、或る数をそれに掛けると総和になるものと考えてもいいかもしれません。m次関数の下の面積を出すとき、シグマ imの曲線は nm+1 があるのでそのままならば無限に増大します。細い長方形の高さを出すときの (1/n)m、幅の (1/n)を掛けると面積が或る値に収束します。シグマの足し算、掛け算の単純さが面積の計算の可能性を保証します。
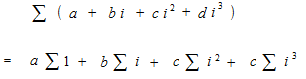
原始人と同じように石を並べてシグマi とシグマ i2を数えます。石を正方形に並べて、ふたつに分けてみます。
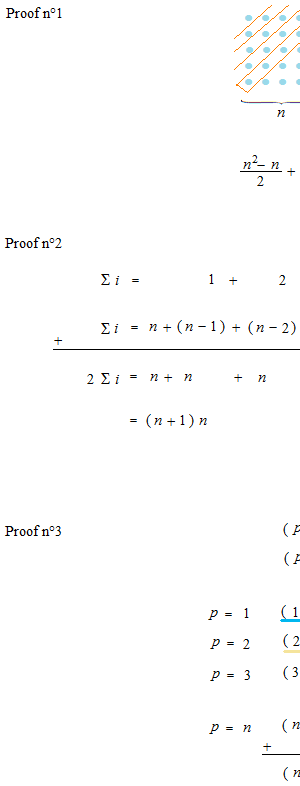
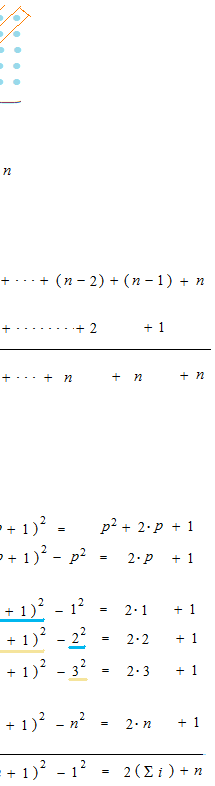
この方法はi の指数が増えていっても使えます。
![]()
シグマの数え方はいろいろあります。図形を使って数える必要はないのですが、三角錐の体積を使うと可能です。立体図形を石が積み重なった物と考えます。三角錐の体積ですが、三角柱を3で割る前に、接面を引いておいてから割って、その後でまた接面を加えます。
この四角錘の石の数を数えようとするわけです。 ふたつに分けます。

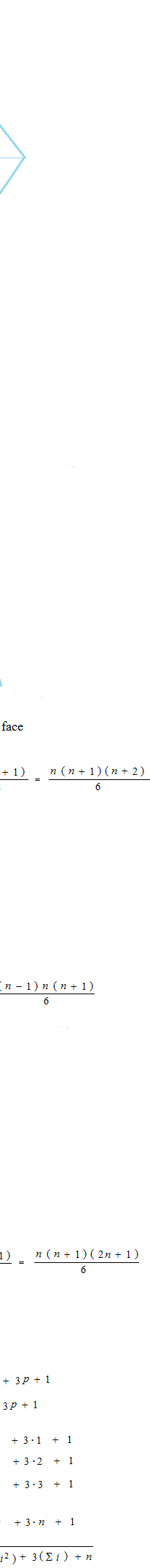
このシグマの数え方は難しい。図式で数えようとすると四次元になってしまいますが、平たくするとたとえばこうなります。
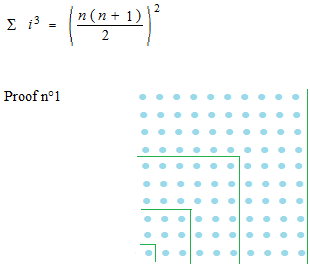
Proof n°2
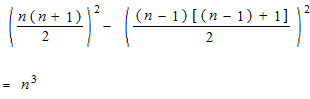
これはずるい。
Proof n°3
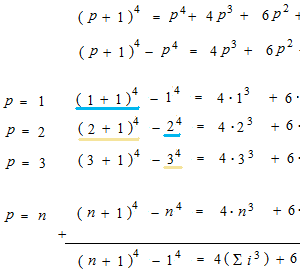
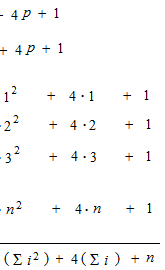
やはりこのシグマの数え方がいいようです。
