George Boole’s Boolean algebra (or Boolean logic)
Here, I made a table of binary functions with two arguments, the values are “coffee” otherwise “orange juice”.
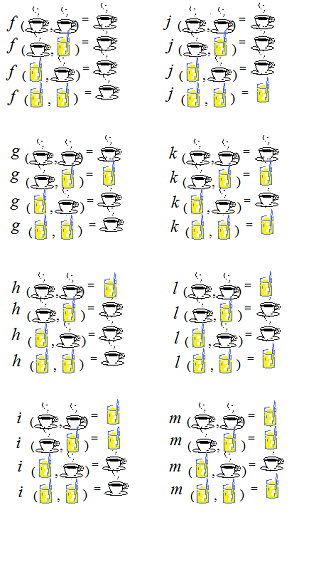
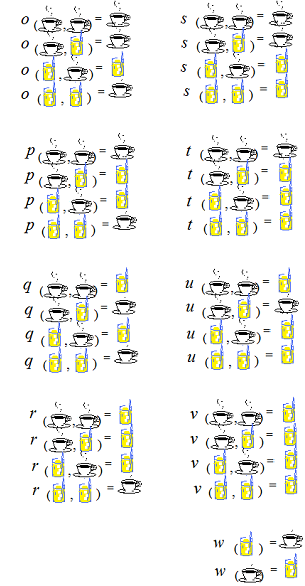
The function j looks like the OR function.
The function t looks like the AND function.
While normal mathematic functions don’t imply variable value in the difinition of that function,
a(x, y) = 4x + 2y
a( 3, 8) = 28
the functionality of a has not been not difined by any particular numbers,
those binary functions imply the variable values as their definition; “When I take a cup of coffee….”, etc. is a part of the functionality. ( In my big English-Japanese dictionary, the word “functionality” doesn’t exist.)
In those binary functions, is there no variable?
Yes, of course, there are variables.
The first argument can be X.
The second argument can be Y.
The values of these variables in a binary logic are very very limited.
Also the image of X and Y under these functions are very very limited. (Image is the “answer” of a function.)
Z can be assigned for image. So, for any function a ,
a(X, Y) = Z
But let’s still keep the values as “coffee” and “orange juice” in our head.
The difference between Boolean algebra and computer’s binary logic is;
while in Boolean algebra, X and Y remain being variabres, which can take everything, even an adjective, as a value, and “1” means all the things in the world or represents the Universe, such as the diagram itself of a Venn’s diagram,
but, in computer’s binary logic, X and Y (or A and B) take only 1 and 0, (or T and F), and “1” means “the addition of the fullness with the emptiness”. ( In my big English-Japanese dictionary, the word “emptiness” doesn’t exist.)
Computer’s binary logic is a special case of Boolean algebra.
The intersection of “all” with “nothing” is “nothing”, because there is no intersection.

In computer’s binary logic, we can not have the value “coffee” otherwise “orange juice”. We have to take a “coffee” otherwise “nothing”, when a cup of coffee is the “all”. So the image of a function can be also “coffee” otherwise “nothing”. (Image is the “answer” of a function.)

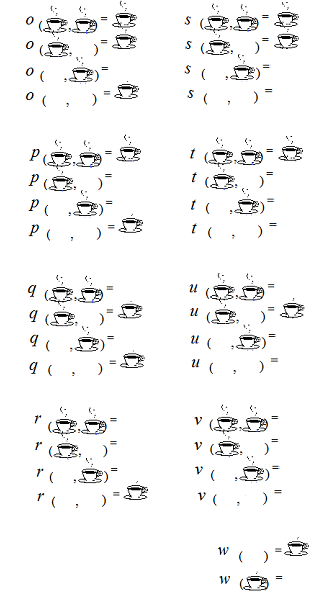
It is better not to use truth tables, because truth tables are only to see the results, there would be no logical thinking, equations. Let’s go back to coffee and orange juice. This page is about Boolean algebra equations, not about binary logic truth tables.
Νομίζω ότι ο Τζώρτζ Μπουλ ήθελε να γίνει μια επέκταση του Αριστοτέλη
ως έκφραση συλλογισμός του στις εξισώσεις.
So, Boolean algebra must start with these things.
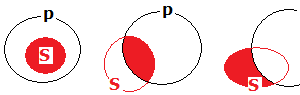
A I O E
The Four Aristotelian Propositions
Universal affirmative A All S is P
Particular affirmative I Some S is P
Particular negative O Some S is not P
Universal negative E All S is not P
Let’s try to understand them without inventing stories, like horses are animals etc. Because it would make affirmative and negative the same story. I mean, “the Japanese are the people with non-blue eyes” and “the Japanese are not the people with blue eyes” would be the same story. That would lose the structural meaning of the Aristotelian Propositions and consider it as a stupidity.
S is a subject and P is a predicate. A subject can be a group of things like “One third of the senators are elected every two years”, and “one third of the senators” is one subject. There for a proposition is talking about ” In which part of the predicate the subject is”.

In Boolean algebra, a predicate is represented small letter x or y or z . That is the key to start the Boolean algebra. George Boole wanted to do an algebra with predicates. A predicate can be an adjective or noun, which has a selective quality. x is not a variable of function. x is not a number. But x is a predicate, which has no quantitative value. Welcome to the non quantitative world of the Logic.
A selection is done by the symbol · , otherwise putting the terms together.
When x is a name Karen. In order to select all Karens in the univers, the symbol · will be used.
1·x
or (1)x
or simply x
In this way x can represent not only a name Karen, but also all Karens in the univers. That is all Xs. They are mostly women, some cats and dogs, some Martiens, etc. They are Xs. These about 10000 individuals make a group; this goup is called class X.
Therefore x can be a predicate, here the name Karen. And x can be also the class X , 10000 Karens in the univers as (1) x .
Now we select the persons that called Karen Philipp.
The name Philipp is y .
xy
y can be a predicate and x can be the class X, namely
y { x (1)}
If there is a Karen every 3000 persons, and there is a Philipp every 4000 persons, there will be a Karen Philipp every 12000000 persons.
( 1 / 3000 ) · ( 1 / 4000 ) = ( 1 / 12000000 )
It looks like selective office of xy and a multiplication by the population universal will be the number of persons who called Karen Philipp. But we must avoid the idea of magnitude.
So as using the symbol 1 , called unity, the symbol of subject S will disappear.

Moreover, a special case, when P is “all” as a predicate.
Predicate z is an adjective that selects “all” of the univers.
z = z (1)
= 1
Welcome to the world of the binary logic. Hello World.
But this page is not for the binary logic, but for the Boolean algebra.
